![[Logo] Instituto Superior Técnico](http://www.math.tecnico.ulisboa.pt/images/logo_ist_class.gif "Instituto Superior Técnico"){kind=logo}
![[Logo] Universidade Técnica de Lisboa](http://www.math.tecnico.ulisboa.pt/images/logoutl2.gif "Universidade Técnica de Lisboa") |
![[Logo] Mathematics Department](http://www.math.tecnico.ulisboa.pt/images/dmtrans.gif "Departamento de Matemática")
|
| .IST
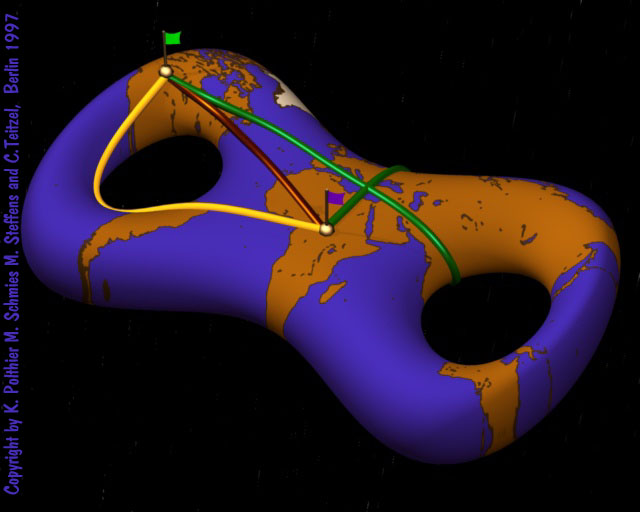
Geometria Riemanniana — 1º Semestre de 2006/2007
Avisos/resumos/pautaJá afixei as notas finais. Podem encontrar mais informação acerca do postulado das paralelas aqui. ProgramaVariedades: variedades diferenciáveis; aplicações diferenciáveis; espaço tangente; imersões e mergulhos; campos vectoriais; fluxos de campos vectoriais; parêntesis de Lie; grupos de Lie; revisão de orientabilidade, variedades com bordo, formas diferenciais, integração em variedades e teorema de Stokes; campos tensoriais. Métricas: variedades Riemannianas; isometrias; métricas invariantes à esquerda; conexões afins; conexão de Levi-Civita; geodésicas; propriedades minimizantes das geodésicas; teorema de Hopf-Rinow. Curvatura: tensor de curvatura; curvatura seccional; tensor de Ricci; curvatura escalar; formas de conexão e de curvatura; equações estruturais de Cartan; índice de um campo vectorial numa singularidade; característica de Euler; teorema de Gauss-Bonnet; imersões isométricas; aplicação de Gauss; curvaturas média e de Gauss; teorema Egregium; primeira e segunda formas fundamentais. Aplicações: relatividade geral. BibliografiaL. Godinho e J. Natário, An Introduction to Riemannian Geometry with Applications, textos de apoio PS, PDF Manfredo Perdigão de Carmo, Geometria Riemanniana, IMPA (1988) Manfredo Perdigão de Carmo, Differential Forms and Applications, Springer (1994) W. Boothby, An Introduction to Differentiable Manifolds and Riemannian Geometry, Academic Press (2003) AvaliaçãoTestes: Haverá dois testes de 1h30m, cada qual com um peso de 35% na nota final, a realizar a meio do semestre e na última semana de aulas. Na semana seguinte os alunos poderão repetir um dos testes para efeito de melhoria de nota. Aulas práticas e trabalhos de casa: Todas as semanas haverá uma lista trabalhos para casa, afixada na página da cadeira, para entregar na semana seguinte. Ao conjunto dos trabalhos de casa será atribuída uma nota, com o peso de 30% na nota final. Exercícios
Pode encontrar mais exercícios nas páginas de Geometria Riemanniana de: TestesLinks |
||||||||||||||||||
|
|