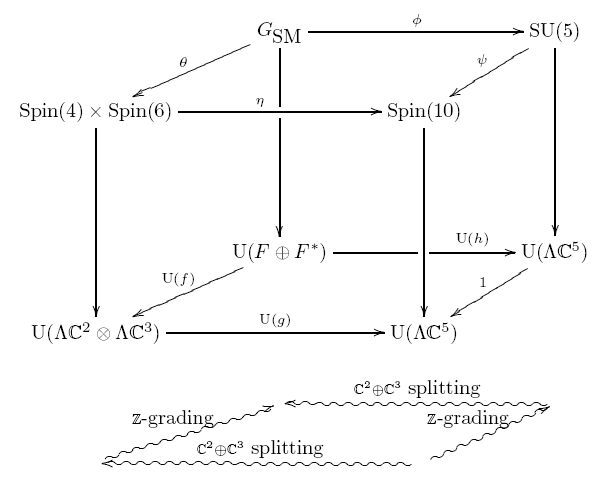
The Standard Model is the best tested and most
widely accepted theory of elementary particles we have today.
It may seem complicated and arbitrary, but it has hidden patterns
that are revealed by the
relationship between three `grand unified theories': theories
that unify forces and particles by extending the Standard Model symmetry
group
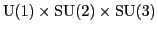
to a
larger group.
These three are Georgi and Glashow's
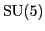
theory,
Georgi's theory based on the group
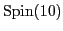
, and the Pati-Salam
model based on the
group
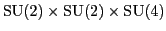
.
In this expository account
for mathematicians, we explain only the portion of these theories that
involves finite-dimensional group representations. This allows us to
reduce the prerequisites to a bare minimum while still giving a
taste of the profound puzzles that physicists are struggling to solve.