Next: 3.4 The Route to Up: 3 Grand Unified Theories Previous: 3.2 The Spin(10) Theory
Next we turn to a unified theory that is not so `grand':
its gauge group is not a simple Lie group, as it was for the
![]() and
and
![]() theories. This theory is called the
Pati-Salam model, after its inventors [28]; it has gauge
group
theories. This theory is called the
Pati-Salam model, after its inventors [28]; it has gauge
group
![]() , which is merely semisimple.
, which is merely semisimple.
We might imagine the ![]() theory as an answer to this question:
theory as an answer to this question:
Why are the hypercharges in the Standard Model what they are?The answer it provides is something like this:
BecauseBut there are other intriguing patterns in the Standard Model thatis the actual gauge group of the world, acting on the representation
.
First, there is a strange similarity between quarks and leptons. Each
generation of fermions in the Standard Model has two quarks and two
leptons. For example, in the first generation we have the quarks ![]() and
and ![]() , and the leptons
, and the leptons ![]() and
and ![]() . The quarks come in three
`colors': this is a picturesque way of saying that they transform in
the fundamental representation of
. The quarks come in three
`colors': this is a picturesque way of saying that they transform in
the fundamental representation of ![]() on
on
![]() . The leptons, on
the other hand, are `white': they transform in the trivial
representation of
. The leptons, on
the other hand, are `white': they transform in the trivial
representation of ![]() on
on ![]() .
.
| Representations of |
|
| Particle | Representation |
| Quark |
|
| Lepton | |
Second, there is a strange difference between left- and right-handed
fermions. The left-handed ones participate in the weak force governed by
![]() , while the right-handed ones do not. Mathematically speaking, the
left-handed ones live in a nontrivial representation of
, while the right-handed ones do not. Mathematically speaking, the
left-handed ones live in a nontrivial representation of ![]() , while the
right-handed ones live in a trivial one. The nontrivial one is
, while the
right-handed ones live in a trivial one. The nontrivial one is
![]() , while
the trivial one is
, while
the trivial one is
![]() :
:
| Representations of |
|
| Particle | Representation |
| Left-handed fermion |
|
| Right-handed fermion |
|
Following Pati and Salam, let us try to sculpt a theory that makes
these ideas precise. In the last two sections, we saw some of the
ingredients we need to make a grand unified theory: we need to extend
the symmetry group
![]() to a larger group
to a larger group ![]() using an inclusion
using an inclusion
![\begin{displaymath}
\xymatrix{
{G_{\mbox{\rm SM}}}\ar[r] \ar[d] & G \ar[d] \\
{\rm U}(F \oplus F^*) \ar[r]^-\sim & {\rm U}(V) \\
}
\end{displaymath}](img561.png)
We now use the same methods to chip away at our current challenge. We
asked if leptons correspond to a fourth color. We already know that
every quark comes in three colors, ![]() ,
, ![]() , and
, and ![]() , which form a basis
for the vector space
, which form a basis
for the vector space
![]() . This is the fundamental representation
of
. This is the fundamental representation
of ![]() , the color symmetry group of the Standard Model. If leptons
correspond to a fourth color, say `white', then we should use the colors
, the color symmetry group of the Standard Model. If leptons
correspond to a fourth color, say `white', then we should use the colors
![]() ,
, ![]() ,
, ![]() and
and ![]() , as a basis for the vector space
, as a basis for the vector space
![]() . This is the
fundamental representation of
. This is the
fundamental representation of ![]() , so let us take that group to
describe color symmetries in our new GUT.
, so let us take that group to
describe color symmetries in our new GUT.
Now ![]() has an obvious inclusion into
has an obvious inclusion into ![]() , using block
diagonal matrices:
, using block
diagonal matrices:
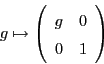
We can do even better if we start with the splitting
So, if we choose a splitting
![]() we should again look at the subgroup that preserves this splitting.
Namely:
we should again look at the subgroup that preserves this splitting.
Namely:
This works very much as it did for ![]() . We want a map
. We want a map
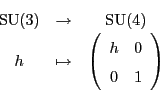
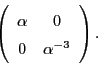
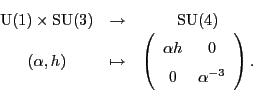
If we let
![]() act on
act on
![]() via this map, the `quark part'
via this map, the `quark part'
![]() transforms as though it has
hypercharge
transforms as though it has
hypercharge ![]() : that is, it gets multiplied by a factor of
: that is, it gets multiplied by a factor of ![]() .
Meanwhile, the `lepton part'
.
Meanwhile, the `lepton part' ![]() transforms as though it has
hypercharge
transforms as though it has
hypercharge ![]() , getting multiplied by a factor of
, getting multiplied by a factor of ![]() .
So, as a representation of
.
So, as a representation of
![]() , we have
, we have
The right-handed leptons do not work this way. That is a problem we need to address. But this brings us to our second question, which was about the strange difference between left- and right-handed particles.
Remember that in the Standard Model, the left-handed particles live
in the fundamental rep of ![]() on
on
![]() , while the right-handed
ones live in the trivial rep on
, while the right-handed
ones live in the trivial rep on
![]() . Physicists write this
by grouping left-handed particles into `doublets', while leaving the
right-handed particles as `singlets':
. Physicists write this
by grouping left-handed particles into `doublets', while leaving the
right-handed particles as `singlets':
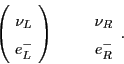

If we restrict these representations to the `left-handed' ![]() subgroup, we obtain:
subgroup, we obtain:
Now let us try to combine these ideas into a theory with symmetry group
![]() . We have seen that letting
. We have seen that letting
![]() act on
act on
![]() is a good way to unify our treatment
of color for all the left-handed fermions. Similarly, the dual representation
on
is a good way to unify our treatment
of color for all the left-handed fermions. Similarly, the dual representation
on
![]() is good for their antiparticles. So, we will tackle color
by letting
is good for their antiparticles. So, we will tackle color
by letting ![]() act on the direct sum
act on the direct sum
![]() . This
space is 8-dimensional. We have also seen that letting
. This
space is 8-dimensional. We have also seen that letting
![]() act on
act on
![]() is a good way to unify our
treatment of isospin for left- and right-handed fermions. This space is
4-dimensional.
is a good way to unify our
treatment of isospin for left- and right-handed fermions. This space is
4-dimensional.
Since
![]() , and the Standard Model representation is
32-dimensional, let us take the tensor product
, and the Standard Model representation is
32-dimensional, let us take the tensor product
How can we map
![]() to
to
![]() ? There
are several possibilities. Our work so far suggests this option:
? There
are several possibilities. Our work so far suggests this option:
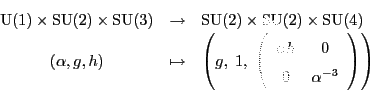
Let us see what this gives. The Pati-Salam representation
of
![]() is a direct sum
of four irreducibles:
is a direct sum
of four irreducibles:
Given our chosen map from
![]() to
to
![]() ,
we can work out which representations of the
,
we can work out which representations of the
![]() these four spaces give.
For example, consider
these four spaces give.
For example, consider ![]() . We have already seen that under our
chosen map,
. We have already seen that under our
chosen map,
If we go ahead and do the other four cases, we see that everything works except for the hypercharges of the right-handed particles--and their antiparticles. Here we just show results for the particles:
| The Pati-Salam Model -- First Try | ||
| Particle | Hypercharge: predicted | Hypercharge: actual |
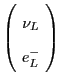 |
||
 |
||
The problem is that the right-handed particles are getting the
same hypercharges as their left-handed brethren.
To fix this problem, we need a more clever map from
![]() to
to
![]() . This map must behave
differently on the
. This map must behave
differently on the ![]() factor of
factor of
![]() , so the hypercharges
come out differently. And it must take advantage of the
right-handed copy of
, so the hypercharges
come out differently. And it must take advantage of the
right-handed copy of ![]() , which acts nontrivially only on the
right-handed particles. For example, we can try this map:
, which acts nontrivially only on the
right-handed particles. For example, we can try this map:
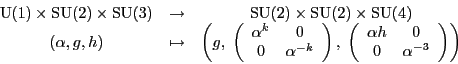
| The Pati-Salam Model -- Second Try | ||
| Particle | Hypercharge: predicted | Hypercharge: actual |
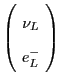 |
||
 |
||
|
|
||
|
|
||
|
|
||
|
|
||
Miraculously, all the hypercharges match if we choose ![]() .
So, let us use this map:
.
So, let us use this map:
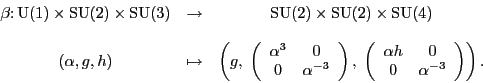
Similarly, we can create a kind of `Pati-Salam code' to specify an
isomorphism of Hilbert spaces
The color comes from
![]() of course, which we already decreed to be spanned
by
of course, which we already decreed to be spanned
by ![]() ,
, ![]() ,
, ![]() and
and ![]() . For antiparticles, we also require anticolors, which
we take to do be the dual basis
. For antiparticles, we also require anticolors, which
we take to do be the dual basis
![]() ,
,
![]() ,
,
![]() and
and
![]() , spanning
, spanning
![]() .
.
It is now easy, with our knowledge of how the Pati-Salam model is to work, to
construct this code. Naturally, the left-handed quark doublet corresponds to
the left-isospin up and down states, which come in all three colors
![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
This table defines an isomorphism of Hilbert spaces
As with ![]() and
and
![]() , we can summarize all the results
of this section in a commutative square:
, we can summarize all the results
of this section in a commutative square:
![\begin{displaymath}
\xymatrix{
{G_{\mbox{\rm SM}}}\ar[r]^-{\beta} \ar[d] & {\rm ...
...s \big({\mathbb C}^4 \oplus {\mathbb C}^{4*}\big)\right) \\
}
\end{displaymath}](img640.png)
The Pati-Salam representation and especially the homomorphism
![]() look less natural than the representation of
look less natural than the representation of ![]() on
on
![]() and the homomorphism
and the homomorphism
![]() .
But appearances can be deceiving: in the next section we shall see
a more elegant way to describe them.
.
But appearances can be deceiving: in the next section we shall see
a more elegant way to describe them.
2010-01-11