Next: 3.2 The Spin(10) Theory Up: 3 Grand Unified Theories Previous: 3 Grand Unified Theories
The ![]() grand unified theory appeared in a 1974 paper by Howard
Georgi and Sheldon Glashow [12]. It was the
first grand unified theory, and is still considered the prototypical
example. As such, there are many accounts of it in the physics
literature. The textbooks by Ross [31] and Mohapatra
[21] both devote an entire chapter to the
grand unified theory appeared in a 1974 paper by Howard
Georgi and Sheldon Glashow [12]. It was the
first grand unified theory, and is still considered the prototypical
example. As such, there are many accounts of it in the physics
literature. The textbooks by Ross [31] and Mohapatra
[21] both devote an entire chapter to the ![]() theory, and a lucid summary can be found in a review article by
Witten [39], which also
discusses the supersymmetric generalization of this theory.
theory, and a lucid summary can be found in a review article by
Witten [39], which also
discusses the supersymmetric generalization of this theory.
In this section, we will limit our attention to the nonsupersymmetric version
of ![]() theory, which is how it was originally proposed. Unfortunately,
this theory has since been ruled out by experiment; it predicts that protons
will decay faster than the current lower bound on proton
lifetime [26]. Nevertheless, because of its prototypical
status and intrinsic interest, we simply must talk about the
theory, which is how it was originally proposed. Unfortunately,
this theory has since been ruled out by experiment; it predicts that protons
will decay faster than the current lower bound on proton
lifetime [26]. Nevertheless, because of its prototypical
status and intrinsic interest, we simply must talk about the ![]() theory.
theory.
The core idea behind the ![]() grand unified theory is that because
the Standard Model representation
grand unified theory is that because
the Standard Model representation ![]() is 32-dimensional,
each particle or antiparticle in the first generation of fermions can
be named by a 5-bit code. Roughly speaking, these bits are the answers
to five yes-or-no questions:
is 32-dimensional,
each particle or antiparticle in the first generation of fermions can
be named by a 5-bit code. Roughly speaking, these bits are the answers
to five yes-or-no questions:
We can flesh out this scheme by demanding that the operation of taking
antiparticles correspond to switching 0's for 1's in the code. So the
code for the antiparticle of ![]() , the `antired right-handed
antidown antiquark', is
, the `antired right-handed
antidown antiquark', is ![]() . This is cute: it means that being
antidown is the same as being up, while being antired is the same as
being both green and blue.
. This is cute: it means that being
antidown is the same as being up, while being antired is the same as
being both green and blue.
Furthermore, in this scheme all antileptons are `black' (the particles with no color, ending in 000), while leptons are `white' (the particles with every color, ending in 111). Quarks have exactly one color, and antiquarks have exactly two.
We are slowly working our way to the ![]() theory. Next let us bring
Hilbert spaces into the game. We can take the basic properties of
being up, down, red, green or blue, and treat them as basis vectors for
theory. Next let us bring
Hilbert spaces into the game. We can take the basic properties of
being up, down, red, green or blue, and treat them as basis vectors for
![]() . Let us call these vectors
. Let us call these vectors ![]() . The exterior algebra
. The exterior algebra
![]() has a basis given by wedge products of these 5 vectors.
This exterior algebra is 32-dimensional, and it has a basis labelled by
5-bit strings. For example, the bit string
has a basis given by wedge products of these 5 vectors.
This exterior algebra is 32-dimensional, and it has a basis labelled by
5-bit strings. For example, the bit string ![]() corresponds to the
basis vector
corresponds to the
basis vector ![]() , while the bit string
, while the bit string ![]() corresponds to
corresponds to
![]() .
.
Next we bring in representation theory. The group ![]() has an
obvious representation on
has an
obvious representation on
![]() . And since the operation of taking
exterior algebras is functorial, this group also has a representation
on
. And since the operation of taking
exterior algebras is functorial, this group also has a representation
on
![]() . In the
. In the ![]() grand unified theory, this is the
representation we use to describe a single generation of fermions and
their antiparticles.
grand unified theory, this is the
representation we use to describe a single generation of fermions and
their antiparticles.
Just by our wording, though, we are picking out a splitting of
![]() into
into
![]() : the isospin and color parts,
respectively. Choosing such a splitting of
: the isospin and color parts,
respectively. Choosing such a splitting of
![]() picks out a subgroup
of
picks out a subgroup
of ![]() , the set of all group elements that preserve this
splitting. This subgroup consists of block diagonal matrices with a
, the set of all group elements that preserve this
splitting. This subgroup consists of block diagonal matrices with a ![]() block and a
block and a ![]() block, both unitary, such that the
determinant of the whole matrix is 1. Let us denote this subgroup as
block, both unitary, such that the
determinant of the whole matrix is 1. Let us denote this subgroup as
![]() .
.
Now for the miracle: the subgroup
![]() is isomorphic
to the Standard Model gauge group (at least modulo a finite subgroup).
And, when we restrict the representation of
is isomorphic
to the Standard Model gauge group (at least modulo a finite subgroup).
And, when we restrict the representation of ![]() on
on
![]() to
to
![]() , we get the Standard Model representation!
, we get the Standard Model representation!
There are two great things about this. The first is that it gives a
concise and mathematically elegant description of the Standard Model
representation. The second is that the seemingly ad hoc hypercharges
in the Standard Model must be exactly what they are for this
description to work. So, physicists say the ![]() theory explains
the fractional charges of quarks: the fact that quark charges come in
units
theory explains
the fractional charges of quarks: the fact that quark charges come in
units ![]() the size of electron charge pops right out of this
theory.
the size of electron charge pops right out of this
theory.
With this foretaste of the fruits the ![]() theory will bear, let
us get to work and sow the seeds. Our work will have two
parts. First we need to check that
theory will bear, let
us get to work and sow the seeds. Our work will have two
parts. First we need to check that
First, the group isomorphism. Naively, one might seek to build
the ![]() theory by including
theory by including
![]() as a subgroup of
as a subgroup of ![]() .
Can this be done?
Clearly, we can include
.
Can this be done?
Clearly, we can include
![]() as block diagonal
matrices in
as block diagonal
matrices in ![]() :
:
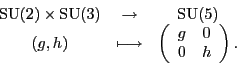
The first clue is that elements of ![]() must commute with the
elements of
must commute with the
elements of
![]() . But the only elements of
. But the only elements of ![]() that commute with everybody in the
that commute with everybody in the
![]() subgroup are
diagonal, since they must separately commute with
subgroup are
diagonal, since they must separately commute with
![]() and
and
![]() , and the only elements doing so are
diagonal. Moreover, they must be scalars on each block. So, they have
to look like this:
, and the only elements doing so are
diagonal. Moreover, they must be scalars on each block. So, they have
to look like this:
So if we throw in elements of this form, do we get
![]() ? More precisely, does this map:
? More precisely, does this map:
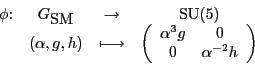
The answer is no: the map ![]() has a kernel,
has a kernel,
![]() .
The kernel is the set of all elements of the form
.
The kernel is the set of all elements of the form
This sets up a nerve-racking test that the ![]() theory must pass
for it to have any chance of success. After all, not all
representations of
theory must pass
for it to have any chance of success. After all, not all
representations of
![]() factor through
factor through
![]() , but all those
coming from representations of
, but all those
coming from representations of ![]() must do so. A representation
of
must do so. A representation
of
![]() will factor through
will factor through
![]() only if the
only if the
![]() subgroup acts
trivially.
subgroup acts
trivially.
In short: the ![]() GUT is doomed unless
GUT is doomed unless
![]() acts trivially on
every fermion. (And antifermion, but that amounts to the same thing.)
For this to be true, some nontrivial relations between hypercharge,
isospin and color must hold.
acts trivially on
every fermion. (And antifermion, but that amounts to the same thing.)
For this to be true, some nontrivial relations between hypercharge,
isospin and color must hold.
For example, consider the left-handed electron
Or, consider the right-handed ![]() quark:
quark:
For ![]() to work, though,
to work, though,
![]() has to act trivially on every
fermion. There are 16 cases to check, and it is an awful lot to demand that
hypercharge, the most erratic part of the Standard Model
representation, satisfies 16 relations.
has to act trivially on every
fermion. There are 16 cases to check, and it is an awful lot to demand that
hypercharge, the most erratic part of the Standard Model
representation, satisfies 16 relations.
Or is it? In general, for a fermion with hypercharge ![]() , there are four
distinct possibilities:
, there are four
distinct possibilities:
| Hypercharge relations | ||||
| Case | Representation | Relation | ||
| Nontrivial |
|
|
||
| Nontrivial |
|
|
||
| Trivial |
|
|
||
| Trivial |
|
|
||
| Hypercharge relations | ||||
| Case | Representation | Relation | ||
| Left-handed quark |
|
|
||
| Left-handed lepton |
|
|
||
| Right-handed quark |
|
|
||
| Right-handed lepton |
|
|
||
| Hypercharge relations | ||
| Case | Relation | |
| Left-handed quark |
|
|
| Left-handed lepton |
|
|
| Right-handed quark |
|
|
| Right-handed lepton |
|
|
By this analysis, we have shown that
![]() acts trivially on the Standard Model
rep, so it is contained in the kernel of this rep. It is better than just a
containment though:
acts trivially on the Standard Model
rep, so it is contained in the kernel of this rep. It is better than just a
containment though:
![]() is the entire kernel. Because of this, we could say
that
is the entire kernel. Because of this, we could say
that
![]() is the `true' gauge group of the Standard Model. And because
we now know that
is the `true' gauge group of the Standard Model. And because
we now know that
Of course, we still need to find a representation of ![]() that extends the
Standard Model representation. Luckily, there is a very beautiful choice
that works: the exterior algebra
that extends the
Standard Model representation. Luckily, there is a very beautiful choice
that works: the exterior algebra
![]() .
Since
.
Since ![]() acts on
acts on
![]() , it has a representation on
, it has a representation on
![]() .
Our next goal is to check that pulling back this representation from
.
Our next goal is to check that pulling back this representation from
![]() to
to
![]() using
using ![]() , we obtain the Stadard model
representation
, we obtain the Stadard model
representation ![]()
As we do this, we will see another fruit of the ![]() theory ripen. The
triviality of
theory ripen. The
triviality of
![]() already imposed some structure on hypercharges,
as outlined in above in Table 3. As we fit the
fermions into
already imposed some structure on hypercharges,
as outlined in above in Table 3. As we fit the
fermions into
![]() , we will see this is no accident: the
hypercharges have to be exactly what they are for the
, we will see this is no accident: the
hypercharges have to be exactly what they are for the
![]() theory to work.
theory to work.
To get started, our strategy will be to use the fact that, being
representations of compact Lie groups, both the fermions ![]() and the exterior algebra
and the exterior algebra
![]() are completely reducible,
so they can be written as a direct sum of irreps. We will then match up
these irreps one at a time.
are completely reducible,
so they can be written as a direct sum of irreps. We will then match up
these irreps one at a time.
The fermions are already written as a direct sum of irreps, so we need
to work on
![]() . Now, any element
. Now, any element
![]() acts as automorphisms
of the exterior algebra
acts as automorphisms
of the exterior algebra
![]() :
:
Let us see how this works, starting with the easiest cases.
![]() and
and
![]() are both trivial irreps of
are both trivial irreps of
![]() . There
are two trivial irreps in the Standard Model representation, namely
. There
are two trivial irreps in the Standard Model representation, namely
![]() and its dual
and its dual
![]() ,
where we use angle brackets to stand for the Hilbert space spanned by
a vector or collection of vectors.
So, we could select
,
where we use angle brackets to stand for the Hilbert space spanned by
a vector or collection of vectors.
So, we could select
![]() and
and
![]() , or vice versa. At this juncture, we
have no reason to prefer one choice to the other.
, or vice versa. At this juncture, we
have no reason to prefer one choice to the other.
Next let us chew on the next piece: the first exterior power,
![]() . We have
. We have
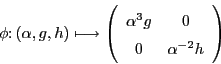
In short, as a rep of
![]() , we have
, we have
Now this is problematic, because another glance at Table 1
reveals that there is no left-handed lepton with
hypercharge 1. The only particles with hypercharge 1 are the right-handed
antileptons, which span the representation
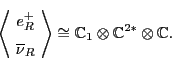
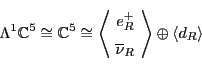
Now we can use our knowledge of the first exterior power to
compute the second exterior power, by applying the formula
So, let us calculate! As reps of
![]() we have
we have
Consider the first summand,
![]() . As a rep of
. As a rep of ![]() this space is just
this space is just
![]() ,
which is the one-dimensional trivial rep,
,
which is the one-dimensional trivial rep, ![]() .
As a rep of
.
As a rep of ![]() it is also trivial. But as a rep of
it is also trivial. But as a rep of
![]() , it is nontrivial. Inside it we are juxtaposing
two particles with hypercharge 1. Hypercharges add, just like charges,
so the composite particle, which consists of one particle and
the other, has hypercharge 2. So, as a representation of the Standard
Model gauge group we have
, it is nontrivial. Inside it we are juxtaposing
two particles with hypercharge 1. Hypercharges add, just like charges,
so the composite particle, which consists of one particle and
the other, has hypercharge 2. So, as a representation of the Standard
Model gauge group we have
Next consider the second summand:
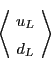
Finally, the third summand in
![]() is
is
In summary, the following pieces of the Standard Model rep
sit inside
![]() :
:
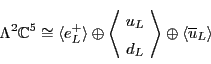
We are almost done. Because ![]() preserves the canonical volume form on
preserves the canonical volume form on
![]() , taking Hodge duals gives an isomorphism between
, taking Hodge duals gives an isomorphism between
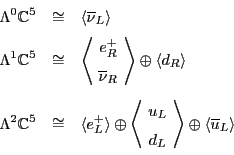
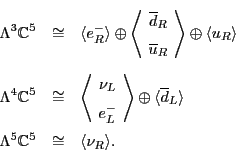
How does all this look in terms of the promised binary code?
Remember, a 5-bit code is short for a wedge product of
basis vectors
![]() . For example, 01101 corresponds
to
. For example, 01101 corresponds
to
![]() . And now that we have found an isomorphism
. And now that we have found an isomorphism
![]() , each of these wedge products corresponds
to a fermion or antifermion. How does this correspondence go, exactly?
, each of these wedge products corresponds
to a fermion or antifermion. How does this correspondence go, exactly?
First consider the grade-one part
![]() .
This has basis vectors called
.
This has basis vectors called ![]() and
and ![]() . We have seen that
the subspace
. We have seen that
the subspace
![]() , spanned by
, spanned by ![]() and
and ![]() , corresponds to
, corresponds to

Next consider the grade-two part:
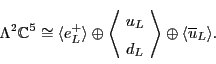
To work out the other grades, note that Hodge duality corresponds to switching
0's and 1's in our binary code. For instance, the dual of 01101 is
10010: or written in terms of basis vectors, the dual of
![]() is
is ![]() . Thus given the binary codes
for the first few exterior powers:
. Thus given the binary codes
for the first few exterior powers:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Now we can see a good, though not decisive, reason to choose
![]() . With this choice, and not the other, we get left-handed particles in
the even grades, and right-handed particles in the odd grades. We choose
to have this pattern now, but later on we need it.
. With this choice, and not the other, we get left-handed particles in
the even grades, and right-handed particles in the odd grades. We choose
to have this pattern now, but later on we need it.
Table 4 defines a linear isomorphism
![]() in terms of the basis vectors, so the equations in this table
are a bit of a exaggeration. When we write say,
in terms of the basis vectors, so the equations in this table
are a bit of a exaggeration. When we write say, ![]() , we really
mean
, we really
mean ![]() . This map
. This map ![]() is an isomorphism between
representations of
is an isomorphism between
representations of
![]() . It tells us how these representations are
the `same'.
. It tells us how these representations are
the `same'.
More precisely, we mean these representations are the same when we
identify
![]() with
with
![]() using the isomorphism
induced by
using the isomorphism
induced by ![]() . In general,
we can think of a unitary representation as a Lie group homomorphism
. In general,
we can think of a unitary representation as a Lie group homomorphism
![\begin{displaymath}
\xymatrix{
{G_{\mbox{\rm SM}}}\ar[r]^\phi \ar[d] & {\rm SU}(...
...rm U}(F \oplus F^*) \ar[r] & {\rm U}(\Lambda {\mathbb C}^5)
}
\end{displaymath}](img467.png)
Indeed, we just showed this! We have seen there exists a
unitary operator from the Standard Model rep to
![]() , say
, say
![\begin{displaymath}
\xymatrix{
{G_{\mbox{\rm SM}}}\ar[r]^\phi \ar[d] & {\rm SU...
...F^*) \ar[r]^-{{\rm U}(f)} & {\rm U}(\Lambda {\mathbb C}^5)
}
\end{displaymath}](img470.png)
2010-01-11