Sample menu:

• Welcome
• News
• Programme
• Committee
• Registration
• Participants
• Social Events
• Photo Gallery
• Location
• Accomodation
• Sponsors
• Contacts

Scientific Programme

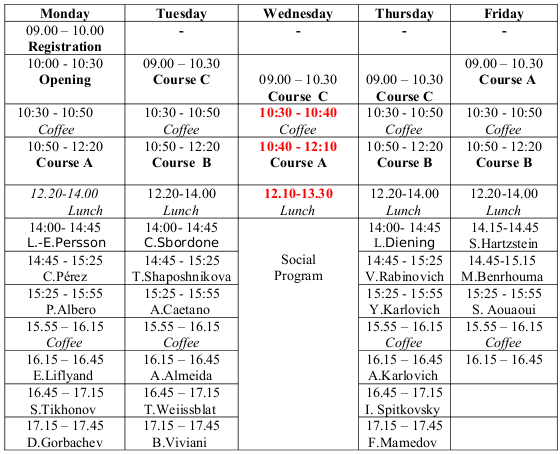
Programme

In the morning we will have summer school lectures. After lunch, invited lecture talks will be given, followed by contributed lectures with the following format:

• 90 minutes for summer school course lectures;
• 45 minutes for invited workshop lectures;
• 40 and 30 minutes for contributed talks.

Programme Overview

Summer School Courses

Each course consists of three sessions of one hour and a half, covering the following topics:

• Course A - Sobolev, capacitary and isocapacitary inequalities
  

  Vladimir Maz'ya - University of Liverpool, UK and University of Linköping, Sweden
  abstract:

  Author's results on the equivalence of various isoperimetric and isocapacitary inequalities, on one hand, and Sobolev's type imbedding and compactness theorems, on the other hand, will be surveyed. Most of the proofs apply to functions on Riemannian manifolds and even very general topological spaces, so that these techniques provide a substitute for the rearrangement methods used to obtain sharp constants in Sobolev's type inequalities in the Euclidean space.

  1. Area minimizing function and Sobolev's type inequalities.
  2. Capacity minimizing function and Sobolev's type inequalities.
  3. Application of capacities to integral inequalities for functions vanishing on a set.

  Lecture slides, Lecture material

• Course B - Weighted problems for operators of harmonic analysis in some Banach function spaces
  

  Vakhtang Kokilashvili - A. Razmadze Mathematical Institute, Georgia
  abstract:

  The aim of our lectures is to discuss the following topics:

  1. Two-weighted estimates for maximal functions, singular integrals and potentials in variable exponent Lebesgue spaces.
  2. Boundedness criteria for the operators of nonlinear harmonic analysis (Cauchy singular integrals, maximal functions defined on rectifiable curves) in weighted grand L^p spaces.
  3. Applications to the Fourier Analysis and boundary value problems for analytic and harmonic functions.

  Lecture notes: Course B

• Course C - Variable Lebesgue Spaces
  

  David Cruz-Uribe, SFO - Trinity College, Hartford, Connecticut, USA
  abstract:

  In these lectures we will explore the properties and applications of the variable Lebesgue spaces L^p(·), also known as the variable exponent spaces.

  1. Banach space properties of the variable Lebesgue spaces. We will consider the structure of these spaces depending on whether the exponent function p(·) is bounded or unbounded, paying particular attention to convergence and duality.
  2. The Hardy-Littlewood maximal operator and extrapolation. We will discuss sufficient conditions on the exponent function p(·) for the maximal operator to be bounded and we will show how Rubio de Francia extrapolation can be used to prove that the classical operators of harmonic analysis are bounded on the variable Lebesgue spaces.
  3. Applications. We will show how the boundedness of the maximal operator and extrapolation can be applied to problems in variable Sobolev spaces and partial differential equations.

  Course C lecture handout: Handout 1, Handout 2, Handout 3

Workshop

Invited Talks

• Bisobolev homeomorphisms and degenerate elliptic systems - Carlo Sbordonne
  abstract:
  Suppose that f = (u; v) is a homeomorphism between planar domains, such that f and its inverse are of Sobolev class W^1,1. We prove that, then, u and v have the same set of critical points a.e.. This allows us to show that to each such f there corresponds a degenerate elliptic matrix A(x) with det A(x) = 1 such that u and v are very weak solutions to the equations div A(x)Du=0 and div A(x)Dv=0. We study planar ACL-homeomorphisms i.e. homeomorphisms f =f(u,v), which are absolutely continuous on lines parallel to the axes together with their inverse. These are results obtained in cooperation with L. Greco, C. Trombetti, N.Fusco, S.Hencl, G. Moscariello, A. Passarelli di Napoli, R. Schiattarella.
• Hardy type inequalities: prehistory, history and some new developments - Lars-Erik Persson
  abstract:
  
  We will first describe something from the dramatic prehistory of 10 years of work until Hardy in 1925 finally proved his famous inequality. In particular, we will shortly describe my own experience when during a summer I wrote the first version of [4] by almost living and feeling as I think Hardy did during this period. After that we will present a "one line convexity proof" of the inequality we now have discovered and developed and which could have changed both the prehistory and history if Hardy had found it. Moreover, we will mention some important problems, results and applications obtained and described in the rich literature in the field, see e.g. the books [1]-[3] and the references given there. Finally, there will be described some very new ideas and also new results recently obtained in collaboration with Natasha Samko and Stefan Samko.
  
  [1] A. Kufner and L.E. Persson, Weighted Inequalities of Hardy Type, World Scientific, New/JerseyLondon/Singapore/Hong Kong, 2003 (357 pages).
  [2] A. Kufner, L. Maligranda and L.E. Persson, The Hardy Inequality. About its History and some Related Results, Vydavatelsky Servis Publishing House, Pilsen, 2007 (161 pages).
  [3] A. Meshki, V. Kokalishvili and L.E. Persson, Weighted Norm Inequalities for Integral Transforms with Product Kernels, Nova Scientific Publishers, Inc., Springer, New York, 2009 (329 pages).
  [4] A. Kufner, L. Maligranda and L.E. Persson,The prehistory of the Hardy inequality, Amer. Math. Monthly 113 (8), 715-732, 2006.
  
• Non-linear Calderon-Zygmund theory for the p-Laplacian including variable exponents - Lars Diening
  abstract:
  It has been possible in the recent years to generalize parts of the linear Calderon-Zymund theory to the non-linear setting of the p-Laplacian. We first discuss the basic principles and results of this method. After that we show how to generalize this to the context of variable exponents.

Contributed Talks

last updated: 01-06-2010

• Capacitary Function Spaces and Interpolation - Pilar Silvestre Albero
• Besov spaces with variable smoothness and integrability - Alexandre Almeida
• Quasilinear elliptic equation with variable exponent coefficients - Sami Aouaoui
• Existence result of sublinear elliptic equation with non-standard growth conditions - Mohamed Benrhouma
• Real interpolation of generalized Besov-Hardy spaces and applications - António Caetano
• Some extremal problems of harmonic analysis for positive definite functions - Dmitry Gorbachev
• The Riesz potential as a multilinear operator into BMO_β spaces - Silvia Ines Hartzstein
• Singular integral operators on Nakano spaces with weights having finite sets of discontinuities - Alexei Karlovich
• Algebras of pseudodifferential operators with non-regular symbols - Yuri Karlovich
• Representation of a function via the absolutely convergent Fourier integral - Elijah Liflyand
• Hardy type inequalities in variable exponent Lebesque space - Farman Mamedov
• Sharp weighted bounds for Singular Integrals and commutators: the A₂ conjecture - Carlos Pérez
• Pseudodifferential operators approach to singular integral operators acting on weighted Lebesgue variable exponent spaces on Carleson curves - Vladimir Rabinovich
• BMO assumptions on the coefficients and the boundary in the Dirichlet problem for higher order elliptic systems - Tatiana Shaposhnikova
• Invertibility properties of some Toeplitz operators with matrix symbols - Ilya Spitkovsky
• Weighted Fourier Inequalities - Sergey Tikhonov
• Global W^2,p estimate for elliptic operator with potential satisfying a reverse Hölder condition - Beatriz Viviani
• On Anisotropic Hardy Spaces - Tal Weissblat

Welcome | News | Programme | Committee | Registration | Participants | Social Events | Location | Accomodation | Sponsors | Contacts

Chairman | Webmaster | Design by Stylish Website Templates