Matemática Computacional

Resumo da matéria [Versão 3.1]

[Capítulo 1] [Capítulo 2] [Capítulo 3] [Capítulo 4] [Capítulo 5]

Capítulo III

Métodos Numéricos para Sistemas

Este capítulo será dividido em três secções principais:

(i) Normas de matrizes e condicionamento
(ii) Métodos iterativos para sistemas lineares
(iii) Métodos iterativos para sistemas não lineares

Normas de matrizes e condicionamento

Normas matriciais induzidas

Iremos considerar normas de matrizes com base em normas vectoriais, ainda que haja normas matriciais que se podem deduzir doutra forma.

Começamos por relembrar as normas vectoriais p (também designadas l ^p) definidas para um vector x ∈ Rⁿ por

∥x∥_p = ( |x₁|^p + |x₂|^p + ... + |x_n|^p ) ^1/p (1 ≤ p < ∞ )

em que os casos mais simples são

norma da soma (p=1)
∥x∥₁ = |x₁| + ... + |x_n|
norma euclidiana (p=2)
∥x∥₂ = ( |x₁|² + ... + |x_n|² ) ^1/2
norma do máximo (p=∞)
∥x∥_∞ = max { |x₁| , ... , |x_n| }
esta última norma surge como limite numérico quando p→∞.

Definição. Seja ∥.∥ uma norma vectorial.
Para uma matrix qualquer x de dimensões n×m definimos a norma matricial induzida por ∥.∥ :

∥A∥ = sup_{x ≠ 0}

∥Ax∥

∥x∥

= max_{∥x∥ = 1} ∥Ax∥

Trata-se de uma norma, sendo fácil verificar que
(i) ∥A∥ ≥ 0; (ii) ∥A∥ = 0 ⇔ A = 0; (iii) ∥α A∥ = |α| ∥A∥; (iv) ∥A + B∥ ≤ ∥A∥ + ∥B∥.
(aqui α representa um qualquer escalar).

Observações:
(a) A igualdade ∥A∥ = max_{∥x∥ = 1} ∥Ax∥ é verificada num espaço de dimensão finita, pois
∥Ax∥ / ∥x∥ = ∥A (x/ ∥x∥)∥ e a condição ∥x∥ = 1 define uma variedade compacta onde há máximo.
(b) É possível definir outras normas não induzidas, é o caso da norma de Fröbenius

∥A∥_F = ( |a₁₁|² + ... + |a_nm|² ) ^1/2

que é uma norma vectorial euclidiana encarando a matriz como um vector de dimensões n × m

Podemos estabelecer propriedades simples, mas importantes para as normas matriciais induzidas:

Proposição Sejam A, B matrizes e x vectores compatíveis.
(a) ∥Ax∥ ≤ ∥A∥ ∥x∥
(b) ∥AB∥ ≤ ∥A∥ ∥B∥

dem:
(a) Porque ∥A∥ ≥ ∥Ax∥/∥x∥, se x≠ 0 e o caso x= 0 é trivial.
(b) Usando (a), ∥ABx∥≤ ∥A∥ ∥Bx∥ obtemos ainda

∥AB∥ = sup_{x≠ 0} ∥ABx∥ / ∥x∥ ≤ sup_{x≠ 0} ∥A∥ ∥Bx∥ / ∥x∥ = ∥A∥ ∥B∥

Observação: Para qualquer norma induzida temos para a matriz identidade

∥ I ∥ = max_∥x∥=1 ∥Ix∥ = 1

e assim também ∥α I∥ = |α|.

Expressões simplificadas de algumas normas matriciais

O cálculo de uma norma pela definição é impraticável, pelo que iremos obter expressões mais simples, especialmente no caso das normas induzidas pela norma do máximo e da soma.

Teorema: Seja A uma matriz n× n, temos

∥A∥_∞ = max_i=1,...,n

n
∑
j=1

|a_ij| ("norma das linhas")

∥A∥₁ = max_j=1,...,n

n
∑
i=1

|a_ij| ("norma das colunas")

Há assim uma relação directa entre a norma das linhas e das colunas:

∥A∥₁ = ∥A^T∥_∞

dem: Demonstramos para a norma do máximo, primeiro ≤ e depois ≥.
Como (Ax)_i = a_{i 1}x₁ + ... + a_{i n}x_n obtemos

∥A∥_∞ = max_{∥x∥_∞ = 1} ∥Ax∥_∞ = max_{∥x∥_∞ = 1} max_i=1,...,n |a_{i 1}x₁ + ... + a_{i n}x_n| ≤ max_i=1,...,n |a_{i 1}| + ... + |a_{i n}|

pois |x_k|≤ ∥x∥_∞.
Falta apenas demonstrar a desigualdade ≥ , ou seja

∥A∥_∞ ≥ |a_{r 1}| + ... + |a_{r n}| = max_i=1,...,n |a_{i 1}| + ... + |a_{i n}|

pois o máximo será atingido numa certa linha r.
Podemos escolher um vector x: ∥x∥_∞ = 1 :

x_j = sign(a_{r j}) ⇐ a_{r j}x_j = a_{r j}sign(a_{r j}) = |a_{r j}|

por isso

∥A∥_∞ ≥ ∥Ax∥_∞ = max_{i=1, ..., n} |a_{i 1}x₁ + ... + a_{i n}x_n| = |a_{r 1}x₁ + ... + a_{r n}x_n| = |a_{r 1}| + ... + |a_{r n}|

A demonstração para a norma da soma é semelhante.

Observação: Há ainda uma expressão explícita para a norma euclidiana induzida

∥A∥₂ =ρ(A^TA)^1/2

onde ρ designa o raio espectral:

Definição: O raio espectral de uma matriz A quadrada n × n é dado por

ρ(A) = max { |λ₁|, ..., |λ_n| }

onde λ₁, ..., λ_n são os valores próprios de A.

Observação:
Os valores próprios podem ser complexos. Quando a matriz é real simétrica, os valores próprios são reais e podemos simplificar:

∥A∥₂ = ρ(A)

(Convém ainda notar que no caso de matrizes complexas, a matriz transposta deve ser substituída pela adjunta A^*=A^T, devendo considerar-se matrizes hermitianas ao invés de simétricas.)

Teorema: (raio espectral como ínfimo de normas induzidas)
Seja A matriz quadrada n × n, temos

ρ(A) ≤ ∥A∥, ∀ ∥.∥ (norma induzida);
∀ ε >0 ∃ ∥.∥ (norma induzida) : ∥A∥≤ ρ(A) +ε ;

No caso em que A é simétrica, o ínfimo é mesmo um mínimo dado por ∥A∥₂=ρ(A).

Erros vectoriais e número de condição matricial

Quando trabalhamos com quantidades vectoriais, dado x um valor exacto e x^~ um valor aproximado, temos as seguintes noções (dependentes da norma considerada):

Erro: e_x(x^~) = x − x^~
Erro absoluto : ∥e_x(x^~)∥ = ∥ x − x^~ ∥
Erro relativo (se x ≠ 0) : ∥δ_x(x^~)∥ com δ_x(x^~) = e_x / ∥x∥

Não havendo ambiguidade e uma só aproximação, abreviamos e_x e δ_x.

Para introduzir o assunto da propagação de erros na resolução de sistemas consideramos um exemplo ilustrativo.

Exemplo
Consideremos a matriz

A =

┌	1	100	-100	┐
│	-1	1	0	│
└	0	-1	1	┘

Começamos por notar que

∥A∥_∞ = max {201, 2, 2} = 201; ∥A∥₁ = max {2, 102, 101} = 102.

Ao resolver o sistema Ax = b com b = (-100, -0.5, 1) obtém-se x = (0, -0.5, 0.5),
mas se introduzimos uma pequena perturbação b^~ = (-100.1, -0.51, 1.1)
o resultado de Ax^~ = b^~ varia dramaticamente: x^~ = (9.9, 9.39, 10.49)
Reparamos que na norma do máximo, temos

∥δ_b∥_∞ = 0.001 e ∥δ_x∥_∞ = 19.98 ⇒ ∥δ_x∥_∞ = 19980 ∥δ_b∥_∞,

um incremento enorme face ao erro inicial.

Esta situação pode ser prevista teoricamente, usando normas matriciais.
Dos sistemas exacto e aproximado,

Ax = b, Ax^~ = b^~

obtemos

A(x − x^~) = b − b^~ ⇒ e_x = A^-1e_b ⇒ ∥e_x∥ ≤ ∥A^-1∥ ∥e_b∥

por outro lado, ∥b∥ = ∥Ax∥ ≤ ∥A∥ ∥x∥ implicando ∥x∥^-1 ≤ ∥A∥ ∥b∥^-1 logo

∥e_x∥

∥x∥

≤ ∥A∥ ∥A^-1∥

∥e_b∥

∥b∥

o factor de escala é ∥A∥ ∥A^-1∥ e isso motiva a definição:

Definição Definimos número de condição da matriz A associado à norma ∥.∥

cond(A) = ∥A∥ ∥A^-1∥

O resultado pode ser traduzido no seguinte teorema

Teorema: Na resolução de sistemas Ax = b verifica-se

cond(A)^-1 ∥δ_b ∥ ≤ ∥δ_x ∥ ≤ cond(A) ∥δ_b ∥

dem: Resta demonstrar a primeira desigualdade, que é deixada como exercício.

Exemplo: Recuperando o exemplo anterior, vemos que

A^-1 =

┌	1	0	100	┐
│	1	1	100	│
└	1	1	101	┘

e portanto

∥A^-1∥_∞ = max {101,102,103} = 103, ∥A^-1∥₁ = max {3,2,301} = 301,

usando os valores calculados anteriormente,

cond_∞(A) = 201×103 = 20703, cond₁(A) = 102×301 = 30702,

e de acordo com o teorema

∥δ_x ∥_∞ ≤ 20703 ∥δ_b ∥_∞

estimativa que se enquadra dentro do factor 19980 que tinhamos obtido.
[Exercício: considerar a norma da soma.]

Observação 1:
Convém notar que este exemplo foi escolhido para evidenciar os possíveis maus resultados devidos a mau condicionamento. Ainda que o número de condição da matriz seja elevado, como se trata apenas de majoração, poderá também haver casos em a propagação de erros esteja bem abaixo desse limite.
Por exemplo, ainda com a mesma matriz, se tivéssemos considerado

b=(1,1,1) aproximado por b^~=(1,1,0.99)

os resultados seriam x=(101,102,103) e x^~=(101,101,101.99) o que significa em termos de erro relativo

∥δ_b ∥_∞=0.01 e ∥δ_x ∥_∞=1.01/103 ≈ 0.01 = ∥δ_b ∥_∞

ou seja, os erros são da mesma dimensão...
− Um número de condição elevado indica a possibilidade de ocorrerem graves perturbações nos resultados, mas isso não significa que elas ocorram forçosamente − depende do vector b.

Observação 2: Tal como foi definido o raio espectral, também podemos definir um número de condição a si associado,

cond_ρ(A) = ρ(A) ρ(A^-1 )

verificando-se cond_ρ(A) ≤ cond(A), pois o raio espectral é o ínfimo das normas induzidas.
A igualdade ocorre para matrizes simétricas, com a norma euclidiana.
− Como os valores próprios de A^-1 são os inversos, temos ainda

cond_ρ(A) =

max ( |λ₁|, ..., |λ_n| )

min ( |λ₁|, ..., |λ_n| )

Observação 3: Em qualquer caso, o número de condição é sempre maior ou igual a 1, pois

1 = ∥ I ∥ = ∥ A A^-1 ∥ ≤ ∥A∥ ∥A^-1∥ = cond(A)

e cond_ρ(A)≥ 1 pela razão entre máximo e mínimo do mesmo conjunto.

Métodos directos − Sistemas lineares

Como acábamos de verificar, mesmo resolvendo exactamente um sistema linear, pequenas perturbações no vector b podem levar a grandes alterações na solução x.
Quando trabalhamos num sistema de ponto flutuante, esses erros são ainda agravados pelos arredondamentos.

Para resolver um sistema com uma matriz qualquer (sem nenhuma estrutura especial) o método de eliminação de Gauss é o mais simples e mais eficaz computacionalmente. O método baseia-se essencialmente numa reconfiguração da matriz A que num passo k será (se o pivot a_kk não for nulo)

a_ij := a_ij − a_ik a_kj / a_kk (i,j = k+1, ..., n)

Reparamos que se tratam de (n-k)² atribuições em cada passo k, e assimptoticamente o método de Gauss envolve

n-1
∑
k=1

(n-k)² ≈ n³/3 (quando n→∞)

muito menos operações que, por exemplo, a Regra de Cramer (≈ n! ).

Por outro lado, a subtracção pode levar a um problema de cancelamento subtractivo.
Esse problema pode ser minorado através de escolha do pivot, em cada passo k efectuando uma troca de linhas/colunas:
− pesquisa total de pivot: escolhe-se a linha/coluna com o máximo |a_ij| (de entre i,j≥ k) e efectua-se uma troca com a linha k e coluna k.
− pesquisa parcial de pivot por linhas: escolhe-se apenas a linha com o máximo |a_ik| (para i≥ k) e efectua-se a troca com a linha k.
Iremos adoptar a pesquisa parcial de pivot por linhas.
O algoritmo resume-se então ao seguinte
Recordamos que para uma matriz quadrada A = [a_ij] de dimensão n, o método se baseia numa factorização A = LU em n-1 passos:
Começamos com [a_ij^[1]] = [a_ij]

Passo k = 1, ..., n-1 : ( obtém-se [a_ij^[k+1]] )
Seja r o índice : |a_{r k}^[k]|=max_{i=k, ..., n}|a_{i k}^[k]|, trocar linhas se r ≠ k
a_{k j}^[k] « a_{r j}^[k] ; b_k^[k] « b_r^[k] ;
Iterar
- para i = k+1, ..., n definir: m_ik = a_ik^[k] / a_kk^[k].
- para i,j = k+1, ..., n
  - a_ij^[k+1] = a_ij^[k] − m_ik a_kj^[k] ;
  - b_i^[k+1] = b_i^[k] − m_ik b_k^[k] ;
Substituição ascendente
- para k = n, ..., 1 (ordem inversa)
  x_k = ( b_k^[k] − n
  ∑
  j=k+1 a_kj^[k] x_j ) / a_kk^[k]

O método de Gauss permite definir uma factorização LU em que

a matriz triangular inferior L = [m_ik] (com i > k)
[considerando ainda L_ii=1, L_ij=0 (se i < j)]
a matriz triangular superior U = [a_kj^[k]] (com j ≥ k)
[considerando ainda U_ij = 0 (se i > j)]

Tendo em atenção a troca de linhas, devemos considerar uma matriz de permutação P, ficando

P A = L U ⇐ P A x = L U x = P b

Uma vez efectuada a factorização, essa poderá ser sempre considerada para outros vectores b^*=P b, resumindo-se a substituições sucessivas:

L y = b^* (substituições descendentes)
U x = y (substituições ascendentes)

cada uma destas substituições envolve ≈ n²/2.

O cálculo da inversa de uma matriz pode ser obtido resolvendo n sistemas da forma

A x^[k] = I^[k] (k= 1, ..., n)

em que I^[k] são as colunas da matriz identidade (vectores da base canónica), e cada solução x^[k] será a coluna correspondente da matriz inversa.

Observação 1: O cálculo da matriz inversa pode ser reduzido a ≈ n³ operações, mas mesmo assim será 3 vezes superior ao cálculo na resolução de um sistema. Assim, é computacionalmente ineficaz resolver um sistema escrevendo x = A^-1b.

Observação 2: A factorização LU pode também ser obtida de forma ligeiramente diferente (método de Doolittle, método de Crout). Para matrizes simétricas definidas positivas pode considerar-se a factorização de Cholesky A=LL^T (ou ainda A=LDL^T).
Noutros contextos, por exemplo cálculo de valores/vectores próprios há utilidade em considerar outras factorizações, como por exemplo a factorização A=QR em que Q é unitária (ou ortogonal, QQ^T=I) e R é triangular superior.

Métodos iterativos − Sistemas lineares

Para além de métodos directos, podem ainda considerar-se métodos iterativos para a resolução de sistemas lineares. Iremos estudar métodos iterativos que resultam da aplicação do método do ponto fixo no caso vectorial.

A ideia mais simples é considerar A = M + N, separando a matriz invertível A numa soma em que M é mais simples de inverter.
Iremos concentrar-nos nos casos:

Método de Jacobi : M = D ; N = L + U;
Método de Gauss-Seidel : M = L + D ; N = U;

em que A = L + D + U, sendo

L a parte triangular inferior de A (L_ij=0 se i ≤ j),
D a parte diagonal de A (D_ij=0 se i ≠ j),
U a parte triangular superior de A (U_ij=0 se i ≥ j).

Resulta então

A x =b ⇔ M x = b − N x

e sendo M invertível, definimos a função iteradora G

A x =b ⇔ x = G(x) = M^-1 ( b − N x )

O método do ponto fixo, x^[k+1] = G(x^[k]), leva ao seguinte método iterativo

x^[k+1] = M^-1 ( b − N x^[k] )

partindo de uma iterada inicial qualquer x^[0]∈R^d (aqui d será a dimensão do espaço).
Estes métodos para sistemas lineares resumem-se a iterações da forma

x^[k+1] = w − C x^[k]

definindo

w = M^-1b ; C = -M^-1N

O ponto fixo será z solução de z = G(z) ⇔ A z =b , que (pela equivalência) é também solução do sistema. O erro verifica

z − x^[k+1] = G(z) − G(x^[k]) = -M^-1N (z − x^[k] )

ou ainda definindo C = -M^-1N

e^[k] = C e^[k-1] = ... = C^k e^[0]

Usando as desigualdades com normas matriciais obtemos também

∥e^[k]∥ ≤ ∥C∥ ∥e^[k-1]∥ ≤ ... ≤ ∥C∥^k ∥e^[0]∥

ficando claro que uma condição suficiente para convergência será exigir que nalguma norma ∥C∥ < 1.
A situação limite será obtida com o raio espectral:

Teorema: (Métodos iterativos para sistemas lineares)
Para qualquer vector inicial x^[0], um método iterativo

x^[k+1]=w + C x^[k]

converge:

(i) se existir uma norma ∥.∥ tal que ∥C∥ < 1

(ii) se e só se ρ(C) < 1

dem: A parte (i) resulta do exposto, resta demonstrar (ii).
Como o raio espectral é ínfimo de normas, dado ε > 0 existe ∥.∥ tal que

∥C∥ < ρ(C) + ε = 1

considerando ε = 1 − ρ(C) > 0, pelo que ρ(C) < 1 é condição suficiente.
Por outro lado, é condição necessária.
Supondo ρ(C) ≥ 1 isto significa |λ| ≥ 1 para algum valor próprio:

Cv=λ v (v ≠ 0)

e escolhendo x^[0] = z − v temos v = e^[0] logo

e^[k] = C^k e^[0] = C^k v = λ^k v

e assim ∥e^[k]∥=|λ|^k ∥v∥ ≥ ∥e^[0]∥ não sendo possível a convergência.

Observação: (Estimativas de Erro)
Como no método do ponto fixo, para além de

∥e^[k]∥ ≤ ∥C∥ ∥e^[k-1]∥ ; ∥e^[k]∥ ≤ ∥C∥^k ∥e^[0]∥

são ainda válidas as estimativas de erro

∥e^[k]∥ ≤

∥C∥

1-∥C∥

∥ x^[k] − x^[k-1] ∥ ; ∥e^[k]∥ ≤

∥C∥^k

1-∥C∥

∥ x^[1] − x^[0] ∥

que são deduzidas de forma semelhante.

As condições suficientes podem ser simplificadas, quando aplicadas a normas específicas. Mais concretamente, é fácil verificar que ∥C∥_∞ < 1 corresponde a exigir que a matriz A tenha diagonal estritamente dominante por linhas:

Definição: Dizemos que uma matriz quadrada A tem a diagonal estritamente dominante por linhas se

|a_ii| >

d
∑
j=1, j ≠ i

|a_ij| (i= 1,...,d)

e terá diagonal estritamente dominante por colunas se

|a_jj| >

d
∑
i=1, i ≠ j

|a_ij| (j= 1,...,d)

Teorema: (Condição suficiente de convergência)
Se uma matriz quadrada tiver a diagonal estritamente dominante por linhas ou por colunas, a matriz é invertível e os métodos de Jacobi e Gauss-Seidel convergem (qualquer que seja a iterada inicial).

dem: Apresentamos a demonstração para o caso da convergência do Método de Jacobi.
Se a diagonal for estritamente dominante por linhas, divindo por |a_ii|,

1 >

d
∑
j=1, j ≠ i

|a_ij|/|a_ii| (i= 1,...,d)

Para o método de Jacobi C = -D^-1(L+U) e assim

C_ii = 0 ; C_ij= − a_ij/a_ii (i ≠ j)

logo

∥C∥_∞ = max_i=1,...,d

d
∑
j=1

|C_ij| = max_i=1,...,d

d
∑
j=1, j≠ i

|a_ij/a_ii| < 1

A condição ∥C∥_∞ < 1 é suficiente para garantir a convergência. Para além disso, a solução será única.
Duas soluções z=G(z), y=G(y) sendo distintas, z ≠ y, implicam

∥z-y∥_∞ = ∥G(z)-G(y)∥_∞ = ∥C(z-y)∥_∞ ≤∥C∥_∞ ∥z-y∥_∞ < ∥z-y∥_∞

ou seja, uma contradição.

Exemplo:
Consideremos um sistema definido pelas 96 equações internas

x_i = (x_i+1 − x_i-1 + x_i+2 − x_i-2)/8 (i=3, ..., 98)

mais 4 equações "nas extremidades"

x₁ = C₁ ; x₂ = C₂ ; x₉₉ = C₃ ; x₁₀₀ = C₄

Dada a forma do sistema, não é preciso identificar a matriz para aplicar o método iterativo de Jacobi

x_i^[k+1] = (x_i+1^[k] − x_i-1^[k] + x_i+2^[k] − x_i-2^[k])/8 (i=3, ..., 98)

as restantes 4 equações das extremidades têm os valores definidos por atribuição directa.
A matriz tem a diagonal estritamente dominante por linhas, e mais concretamente ∥C∥_∞ = 4× 1/8 = 0.5, concluindo-se a convergência do método.
Portanto, começando com x_i^[0] = 0 para i=3, ..., 98, obtemos ainda

x_i^[1] = 0 para i=5, ..., 96,

com

x₃^[1]= -(C₁+C₂)/8 ; x₄^[1]= -C₂/8 ; x₉₈^[1]= (C₃+C₄)/8 ; x₉₇^[1]= C₃/8 ;

Sendo

∥x^[1] − x^[0]∥_∞ =

max{ |C₁+C₂|, |C₃+C₄|, |C₂|, |C₃| } = C_M

obtemos a estimativa a priori

∥e^[k]∥_∞ ≤ 0.5^k-1 C_M

Método SOR

O método SOR (sucessive over-relaxation) é uma generalização do método de Gauss-Seidel, dependente de um parâmetro ω ∈ ]0,2[.
Este método faz parte de uma técnica de relaxação cuja ideia é introduzir um parâmetro livre que pode melhorar a prestação do método original. Mais precisamente, considera-se a combinação "convexa" entre o método iterativo e a identidade enquanto função iteradora:

x^[k+1]=G(x^[k]) e x^[k+1]=x^[k] ,

através do parâmetro de relaxação ω, obtendo-se

x^[k+1] = (1 − ω) x^[k] + ω (G(x^[k]).

Convém notar que ω = 0 não tem significado enquanto método iterativo, e como ω = 1 remete ao método original, o parâmetro é considerado no intervalo aí centrado, ou seja ω ∈ ]0,2[.

A técnica de relaxação aplicada ao método de Gauss-Seidel é semelhante, mas evitando a inversa de L+D, ou seja,

x^[k+1]= (1 − ω) x^[k] + ω D^-1(b − L x^[k+1] − U x^[k] ).

Esta iteração é designada como método SOR.

É claro que para ω=1 sendo o método SOR igual ao método de Gauss-Seidel, as condições de convergência são as mesmas.
Por outro lado, como podemos escrever de forma equivalente

ω^-1 D x^[k+1] = (1 − ω)/ω Dx^[k] + (b − L x^[k+1] − U x^[k] ).

ou seja,

(L + ω^-1D)x^[k+1]= b − (U + (1 − ω^-1)D)x^[k].

identificando-se as matrizes M e N :

M_ω = L + ω^-1D
N_ω = U + (1-ω^-1)D
e consequentemente
C_ω = -M_ω^-1N_ω

Conclui-se assim que a condição necessária e suficiente para a convergência do método SOR é verificar

ρ (C_ω) < 1,

podendo ainda enunciar-se uma outra condição suficiente de convergência:

Teorema: Seja A uma matriz simétrica e definida positiva. O método SOR converge para a solução do sistema, qualquer que seja ω∈ ]0,2[.

Em particular também se conclui que o método de Gauss-Seidel é convergente quando as matrizes são simétricas e definidas positivas.

Exemplo: Consideremos a matriz simétrica e definida positiva

A =

┌	252	-73	-20	60	┐
│	-73	97	47	-89	│
│	-20	47	276	78	│
└	60	-89	78	186	┘

Aplicando o método SOR e calculando o raio espectral em função de ω, ou seja a função

ω ↦ ρ (C_ω)

obtemos o gráfico da Figura 1, onde se torna claro que o raio espectral é sempre inferior a 1, para valores ω ∈ ]0,2[. O valor mínimo é atingido num valor optimal ω^*. Para esta matriz vemos pelo gráfico que ω^*≈ 1.36 e que reduz para quase metade (ρ(C_ω*) ≈ 0.41) o valor do raio espectral no método de Gauss-Seidel (ρ(C₁) ≈ 0.80), permitindo duplicar a rapidez de convergência.

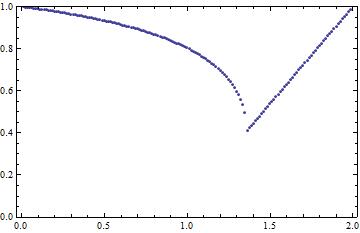
Figura 1: Variação de ρ(C_ω*) em função do parâmetro ω.

Métodos para Sistemas não Lineares

Os métodos iterativos para sistemas lineares, que acabamos de ver, são um caso particular da aplicação do Método do Ponto Fixo a problemas vectoriais. De facto, o Método do Ponto Fixo pode ser generalizado a problemas vectoriais não lineares, e até a problemas com operadores em dimensão infinita.

Método do Ponto Fixo − Vectorial

Consideremos um sistema na forma genérica f(x) = 0 em que estabelecemos uma equivalência com um sistema x = g(x), i.e. em termos de componentes:

╭
│	f₁(x₁, ...,x_N) = 0
┤	...
│	f_N(x₁, ...,x_N) = 0
╰

⇔

╭
│	x₁ = g₁(x₁, ...,x_N)
┤	...
│	x_N = g_N(x₁, ...,x_N)
╰

De forma semelhante, o Método do Ponto Fixo considera a iteração

Dado um vector inicial x^[0]
Iterar x^[k+1] = G(x^[k])

A convergência está ainda ligada à noção de contractividade, que é agora associada a alguma norma.

Definição: Seja Ω ⊆ R^N um conjunto fechado, onde para uma certa norma ∥.∥ se verifica

∃ 0 < L < 1 : ∥ G(x) − G(y) ∥ ≤ L ∥x − y∥ ∀ x, y∈ Ω

então diz-se que a função vectorial iteradora G é contractiva em Ω na norma ∥.∥ (com constante de contractividade L < 1).

É ainda possível estabelecer uma relação entre esta noção de contractividade e as derivadas, através da norma da matriz jacobiana. Relembramos que a matriz jacobiana de G é dada pelas derivadas parciais:

DG =

┌	∂g₁/∂x₁	...	∂g₁/∂x_N	┐
│	...		...	│
└	∂g_N/∂x₁	...	∂g_N/∂x_N	┘

Convém notar que há uma ordenação por linhas, e que se trata de uma matriz de funções, que será depois uma matriz de números DG(x) quando avaliada num ponto x = (x₁, ..., x_N) específico.

Teorema: Seja Ω ⊆ R^N um conjunto fechado e convexo (e com interior não vazio), onde para uma certa norma ∥.∥ se verifica

∃ 0 < L < 1 : ∥ DG(x) ∥ ≤ L ∀ x∈ Ω

então a função vectorial iteradora G é contractiva em Ω nessa norma.

dem: Recordamos que Ω é um conjunto convexo se

∀ x, y ∈ Ω, [x, y] = { x + α(y − x) : α ∈ [0, 1]} ⊆ Ω

Ou seja, quando dois pontos estão no conjunto, o segmento [x, y] está ainda nesse conjunto.
Esta restrição é importante para a existência de ξ_k∈ [x, y] tal que

g_k(x) = g_k(y) + ∇g_k(ξ_k)⋅(x − y)

Dessa forma, como DG = [ ∇ g_k]_k (gradientes nas linhas), obtemos

∥G(x) − G(y)∥ ≤ ∥DG(ξ^*)∥ ∥x − y∥ ≤ L ∥x − y∥

notando que aqui simplificámos bastante ao omitir os detalhes que permitem definir um ξ^*∈ Ω a partir dos diferentes ξ_k∈ [x, y].

Podemos reparar que no caso de sistemas lineares, ao definir uma função iteradora G(x) = w + Cx obtemos

DG = C

pelo que a condição ∥C∥ < 1 corresponde a exigir que essa função iteradora seja contractiva.

Teorema do Ponto Fixo: (em R^N)
Seja Ω ⊆ R^N um conjunto fechado (com interior não vazio), onde para uma certa norma ∥.∥ se verifica

G é contractiva
G é invariante (ou seja, G(Ω)⊆Ω )

então existe um único ponto fixo z∈Ω, e há convergência do método do ponto fixo, qualquer que seja o x^[0]∈Ω.

dem: A única diferença na demonstração (face ao caso linear) será a parte de existência, que resulta de mostrar que a sucessão definida pelo método do ponto fixo é sucessão de Cauchy. De resto, a parte de unicidade é semelhante, e também obtemos

∥e^[k+1]∥ = ∥z − x^[k+1]∥ = ∥G(z) − G(x^[k])∥ ≤ L ∥z − x^[k]∥ = L ∥e^[k]∥

concluindo-se a convergência, pois ∥e^[k]∥ = L^k ∥e^[0]∥ converge para zero quando L < 1.

Observação: (Estimativas de Erro)
Como anteriormente, para além de

∥e^[k]∥ ≤ L ∥e^[k-1]∥ ; ∥e^[k]∥ ≤ L^k ∥e^[0]∥

são ainda válidas as estimativas de erro

∥e^[k]∥ ≤

1 − L

∥ x^[k] − x^[k-1] ∥ ; ∥e^[k]∥ ≤

L^k

1 − L

∥ x^[1] − x^[0] ∥

que são deduzidas de forma semelhante.

Exemplo:
Para L = max{|a|,|b|} < 1, consideremos

G(x) = ( cos(ax₂), sin(bx₁) )

Facilmente obtemos

DG(x) =

┌			┐
│	0	-a sin(ax₂)	│
│	b cos(bx₁)	0	│
└			┘

⇒ ∥DG(x)∥_∞ ≤ max{|a|,|b|}

e podemos concluir, pelo Teorema do Ponto Fixo, que a função G tem um só ponto fixo em R² (porque o espaço todo é fechado e convexo), quando |a|, |b| < 1.
Tendo em atenção que G(R²) ⊆ [-1,1]² podemos concluir que o ponto fixo estará sempre nesse quadrado.

Por exemplo, se a=b=1/2, e começando com x^[0]=0 obtemos sucessivamente

x^[1]=(1,0); x^[2]=(1, 0.4794… ); x^[3]=(0.9174… , 0.4794… );

Como ∥DG(x)∥_∞ ≤ L = 1/2, daqui resulta,

∥e^[3]∥_∞ ≤ ∥ x^[3] − x^[2] ∥_∞ = 0.0836…

Método de Newton generalizado

Consideramos agora uma generalização do Método de Newton para o caso vectorial.
Se a função F for diferenciável, com matriz Jacobiana invertível, podemos estabelecer a equivalência

F(x)=0 ⇔ [DF(x)]^-1F(x)=0 ⇔ x = x − [DF(x)]^-1F(x)

A função iteradora G(x) = x − [DF(x)]^-1F(x) define o Método de Newton

Dado um vector inicial x^[0]
Iteramos
x^[k+1] = x^[k] − [DF(x^[k])]^-1F(x^[k])
ou ainda, para evitar inverter a matriz, resolvemos o sistema
[DF(x^[k])](d^[k]) = -F(x^[k])
em que d^[k] = x^[k+1]-x^[k] ⇔ x^[k+1] = x^[k] + d^[k]
o que é computacionalmente mais eficaz.

Observação: Não pretendendo entrar em detalhe, é possível demonstrar que localmente (e quando a matriz Jacobiana é invertível) o Método de Newton apresenta convergência pelo menos quadrática, no sentido

∥e^[k+1]∥ ≤ K ∥e^[k]∥²

onde K é uma constante que depende da limitação das 2ªs derivadas de F (tal como ocorria no caso escalar).