Matemática Computacional

Resumo da matéria [Versão 3.1]

[Capítulo 1] [Capítulo 2] [Capítulo 3] [Capítulo 4] [Capítulo 5]

Capítulo II

Métodos para Equações não Lineares

A resolução de equações algébricas (polinomiais) foi um assunto que interessou mesmo às civilizações mais antigas. É possível encontrar registos nos Babilónios (séc.IV AC) e em Euclides (séc.III AC) de métodos para resolver algumas equações de segundo grau (ver ainda as contribuições hindus por Brahmagupta, séc.VII, e árabes por Al-Kharizmi, séc.IX).
No entanto a procura de uma fórmula resolvente para equações do terceiro grau resistiu milénios. Os progressos árabes e medievais só foram concretizados no séc. XVI, no Renascimento italiano.
Posteriormente novas dificuldades (e impossibilidades) para encontrar fórmulas resolventes gerais levaram a que fossem estabelecidos métodos numéricos para a resolução de quaisquer equações.
Ao mesmo tempo, estes métodos numéricos revelavam um cálculo mais eficaz do que a utilização das próprias fórmulas resolventes e não tinham a limitação de estarem restritos a equações algébricas.

Equações Algébricas

1º Grau: As equações do primeiro grau têm uma resolução aparentemente trivial:
a x + b = 0 ⇔ x = -a^-1 b (quando a ≠ 0)
Convém notar que mesmo neste caso trivial, está presente um algoritmo de divisão em b/a, bem conhecido desde os primeiros tempos de escola, mas que num sistema FP não é propriamente trivial de implementar (a sua programação genérica será até mais complicada que a dos restantes algoritmos que abordaremos neste curso).
Para além disso, ao escrever a solução na forma x = -a^-1 b, incluímos um caso geral, que contém matrizes, onde a condição a ≠ 0, passa a ser uma condição de invertibilidade det(a) ≠ 0.
2º Grau: As equações do segundo grau têm também uma resolução simples:
a x² + b x + c = 0 ⇔ x = (2a)^-1 ( - b ± (b² − 4ac)^1/2 ) (quando a ≠ 0)
As soluções podem ser complexas se o discriminante for negativo, b² − 4ac < 0.
Esta expressão contém uma resolução mais geral numa estrutura de corpo (p. ex: matrizes diagonais).
3º e 4º Grau: Após lentos progressos medievais, del Ferro e Tartaglia encontraram a fórmula resolvente para a equação do 3º grau, no séc.XVI. Na mesma altura, com técnicas semelhantes, G. Cardan e L. Ferrari deduziram a fórmula do 4º grau e ambas foram publicitadas por Cardan.
Links para expressões destas fórmulas resolventes: 3º grau , 4º grau. As técnicas da Universidade de Bolonha falharam durante os séculos seguintes para equações de quinto grau (ou superior).
5º Grau: Encontrar ou não a fórmula resolvente para a equação do 5º Grau foi um dos problemas mais importantes nos 3 séculos seguintes. Após progressos significativos de Lagrange, a resposta de impossibilidade foi provada independentemente por Galois e Abel (início do séc. XIX).
Esta resposta de impossibilidade de haver fórmulas resolventes para equações algébricas de grau 5 ou superior, tornou claro que não haveria possibilidade de exprimir soluções exactas de forma algébrica exacta.
Grau p: Apesar da inexistência de fórmula resolvente (para grau ≥ 5) foi estabelecido analiticamente ( Argand, Gauss, início do séc. XIX) que as equações algébricas de grau p teriam exactamente p raízes complexas − é o denominado teorema fundamental da álgebra.

Equações não algébricas: A questão de encontrar fórmulas resolventes apenas se colocava para equações polinomiais, colocando de fora todas as equações que envolveriam outras funções, como senos, co-senos, exponenciais, logaritmos, etc... Para além disso essas equações envolviam soluções transcendentes, números que não são solução de nenhuma equação algébrica, como é o caso de π ou de e.

Métodos Numéricos
Com as dificuldades na obtenção de fórmulas resolventes, algumas técnicas numéricas eram usadas, já mesmo antes do Renascimento. Fibonacci (séc. XIII) apresenta resultados nesse sentido (iterações de ponto fixo) para algumas equações algébricas, ainda que de forma dispersa e não sistematizada.
Foi só com o advento do cálculo, no séc. XVII, que os métodos numéricos foram bem estabelecidos, através dos trabalhos de Newton (ver também Raphson). O Método de Newton, que iremos estudar, é ainda hoje um dos métodos mais utilizados.
Não havendo fórmula resolvente, a única possibilidade efectiva de determinar soluções de equações algébricas, ou não algébricas, é através métodos numéricos.

Formulação genérica:
Dada uma função real f ∈ C[a,b], pretendemos aproximar soluções z ∈ [a,b] que verifiquem

f ( z ) = 0

As soluções z são também designadas raízes ou ainda zeros da função f.

Os métodos iterativos consistem em encontrar uma sucessão (x_n) que convirja para a solução z. Essa sucessão é contruída de forma recursiva (ou iterativa), começando com valores iniciais e calculando o valor x_n+1 a partir do anterior x_n (ou anteriores, x_n, x_n-1, ...)
Convém notar que uma vez estabelecida a convergência da sucessão (x_n) temos não apenas uma aproximação em cada termo x_n, mas também um representante exacto do número real através da sucessão convergente de racionais (se os valores x_n forem reais, podemos sempre tomar uma boa aproximação racional que não influi na convergência).
Com as devidas adaptações os métodos que apresentamos neste capítulo para intervalos reais podem ser considerados em contextos muito mais gerais. (O método mais limitado na generalização é o método da bissecção, pois necessita de uma ordenação; os restantes podem ser generalizados ao caso complexo, ao caso matricial, ao caso de operadores, etc.)

Começamos por rever alguns resultados de Análise que permitem assegurar unicidade e existência (não construtiva) de solução para uma equação qualquer num intervalo.

Localização de Raízes

Se for possível esboçar o gráfico da função, podemos ter uma ideia aproximada da localização das raízes, mas para assegurarmos rigorosamente que, num intervalo, existe uma e uma só raiz, recordamos alguns teoremas elementares da Análise:

Teorema (Existência − Valor Intermédio):
Seja f ∈ C[a,b] : f(a) f(b) ≤ 0. Então ∃ z ∈ [a,b] : f(z) = 0.

O teorema do valor intermédio garante apenas a existência, para garantir unicidade, podemos usar :

Teorema (Unicidade − Rolle) :
Seja f ∈ C¹ [a,b]. Se f '(x)≠ 0 ∀ x ∈ [a,b] então f é estritamente monótona em [a,b].
Se f é estritamente monótona, existe no máximo um zero de f nesse intervalo.

Usando apenas o teorema do valor médio de Lagrange podemos obter uma estimativa de erro a posteriori para um valor aproximado qualquer.

Teorema (do Valor Médio de Lagrange):
Seja f ∈ C¹ [a,b]. Então ∃ ξ ∈ [a,b]: f(a)-f(b) = f '(ξ) (a-b)
Corolário (Estimativa de erro a posteriori):
Seja f ∈ C¹ [a,b] com f '(x) ≠ 0 ∀ x∈ [a,b].
Se z^~ é uma aproximação da raiz z em [a,b], então

|z − z^~| ≤

| f(z^~)|

min_x∈[a,b]|f '(x)|

dem:
Como z , z^~∈ [a,b] existe ξ∈ [z; z^~ ] ⊆ [a,b]:

f(z^~) − f(z) = f '(ξ)(z^~ − z)

e como f(z)=0, temos |z^~ − z| = |f(z^~)| / |f '(ξ)|, logo

|z − z^~| ≤ |f(z^~)| / min_x∈[a,b] |f '(x)|.

Estes teoremas não nos dão um método para aproximar ou construir a solução do problema. No entanto, podemos basear-nos no teorema do valor intermédio para desenvolver um método iterativo ("sempre") convergente muito simples.

Método da Bissecção

Assumimos que no intervalo [a, b] a equação f(x) = 0 tem apenas uma e uma só raiz (o que pode ser verificado pelos dois primeiros teoremas anteriores.
Construímos intervalos [ a_n, b_n ] com metade do comprimento dos anteriores [ a_n-1, b_n-1 ], onde asseguramos a existência da raiz, pelo Teorema do valor intermédio.

O método pode-se esquematizar num ciclo :

Intervalo Inicial : [ a₀ , b₀ ] = [ a, b ]
Iterar − Passo n=1, 2, ... :

No final de um passo n temos uma aproximação x_n e o consequente erro de aproximação

e_n = z − x_n

e podemos obter uma estimativa de erro a posteriori usando o Corolário anterior,

|e_n| ≤ |f(x_n)| / min_{x∈[a_n-1, b_n-1]} |f '(x)| ,

mas podemos também deduzir estimativas a priori.

Estimativa a priori no método da bissecção.
Como x_n é o ponto médio, o novo intervalo [ a_n, b_n ] tem metade do comprimento do anterior [ a_n-1, b_n-1 ],
|a_n − b_n| = ½|a_n-1 − b_n-1 |
e assim sucessivamente
|a_n − b_n| = (½)ⁿ|a₀ − b₀ | = 2^-n|a − b| .
Por outro lado, z∈ [ a_n, b_n ], com x_n=a_n ou x_n=b_n,
|e_n| = |z − x_n| ≤ |a_n − b_n| = 2^-n|a − b| .
que é uma estimativa a priori (podemos majorar o erro absoluto no passo n sem calcular nenhuma iteração).
Se pretendermos que |e_n| ≤ ε basta exigir a priori que
2^-n|a − b| ≤ ε ⇔ |a − b| / ε ≤ 2ⁿ
⇔ n ≥ log ₂ ( |a − b| / ε )
Concluímos, por exemplo, que para um intervalo unitário |a − b|=1, a precisão dupla é garantida ao fim de pouco mais de cinquenta iterações, porque para ε < 2^-56≈ 1.4× 10^-17 bastará n > 56.

O método da bissecção pode ser sempre utilizado como um método de recurso, mas iremos estudar uma classe de métodos que podem apresentar uma rapidez de convergência muito superior, ao ponto de reduzir bastante as mais de cinquenta iterações estimadas para o método da bissecção atingir precisão dupla (partindo dum intervalo unitário). Essa classe são os métodos de ponto fixo, cujo método de Newton é um caso particular (e frequentemente atinge precisão dupla em cinco iterações).

Método do Ponto Fixo

O método do ponto fixo consiste em estabelecer uma equivalência

f(z)=0 ⇔ z=g(z)

em que o zero z da função f é o ponto fixo duma outra função g (denominada função iteradora). Depois, o método resume-se à iteração:

Dado um x₀ inicial qualquer;
Iterar x_n+1=g(x_n).

Exemplos:

Numa máquina de calcular, começando com 0 (ou qualquer outro valor), se carregarmos sucessivamente na tecla COS, obtemos uma sucessão de valores (em radianos)
0; 1.0 ; 0.54… ; 0.857… ; ... ; 0.737… ; ... ; 0.73907… ; ... ; 0.7390851… ; etc...
Em menos de 50 iterações vemos que a sucessão de valores começa a estabilizar e os primeiros dígitos não se alteram.
- Neste processo estamos a aplicar o método do ponto fixo, em que a função iteradora é a função co-seno.
  Começámos com x₀=0 e fazemos repetidamente x_n+1= cos (x_n).
- Havendo convergência (é o caso), x_n → z e então
  cos (x_n)→ cos (z)
  porque o co-seno é função contínua. Assim, no limite
  x_n+1= cos (x_n) → z = cos (z).
  Concluímos que o valor limite z=0.7390851… será solução da equação z = cos (z).
- Sendo f(x) = x − cos (x) temos
  f(x) = 0 ⇔ x = g(x) = cos (x).
  Aplicando os teoremas anteriores podemos ver que no intervalo [0,1] temos
  f(0) = 0 − cos(0) = -1 < 0, f(1) = 1 − cos(1) > 0
  concluindo-se a existência de solução. A unicidade resulta de f '(x)= 1 + sin (x)≥ 0 e que só é nula quando x=π/2+k π ∉ [0,1].
- Para além disso, como
  min_x∈[0,1] |f '(x)| = min_x∈[0,1] |1+ sin (x)| = 1
  a estimativa a posteriori permite concluir imediatamente que o erro absoluto para o último valor apresentado é muito pequeno:
  |z − 0.7390851…| ≤ ^{|0.7390851… − cos (0.7390851…)|}_/₁ = 0.55…× 10^-7
Outros exemplos ocorrem carregando sucessivamente noutras teclas. Considerando por exemplo uma tecla para a raiz quadrada, obtemos g(x)=√ x e a sucessão x_n+1=√ x_n converge para uma solução de z=√ z, ou ainda z=z², que é z=1. Neste caso há ainda uma solução z=0 mas o método nunca converge para esse valor, a menos que se comece exactamente com esse valor.
Por outro lado, se houver uma tecla para o quadrado, obtemos g(x)=x² e a sucessão x_n+1=x_n² converge para uma solução de z=z², que é z=0 apenas se |x₀| < 1. Se por outro lado |x₀| > 1 a sucessão tenderá para infinito. A iteração apenas atinge a outra solução z=1 quando começamos com x₀=± 1.

Vemos assim que há casos distintos, de convergência e não convergência, que iremos analisar. De um modo genérico, a "tecla" que se carrega sucessivamente será a função iteradora g. O valor que aparece inicialmente é a iterada inicial, e posteriormente uma análise empírica de convergência pode ser considerada se a sucessão de valores for estabilizando consecutivamente os dígitos.

Observação: Independentemente da convergência, a qualquer momento podemos avaliar o erro de uma qualquer iterada, aplicando a estimativa a priori para f(x)= x − g(x) e z^~=x_n:

|z − x_n| ≤

| x_n − g(x_n)|

min_x∈[a,b]|1 − g'(x)|

≤

| x_n+1 − x_n|

1 − max_x∈[a,b]|g'(x)|

quando |g'(x)| < 1, condição que se revela determinante na convergência.

Baseados nos gráficos genéricos de várias funções g podemos observar na Figura 1 iterações que explicitam casos de convergência e de "divergência" (ou não convergência).

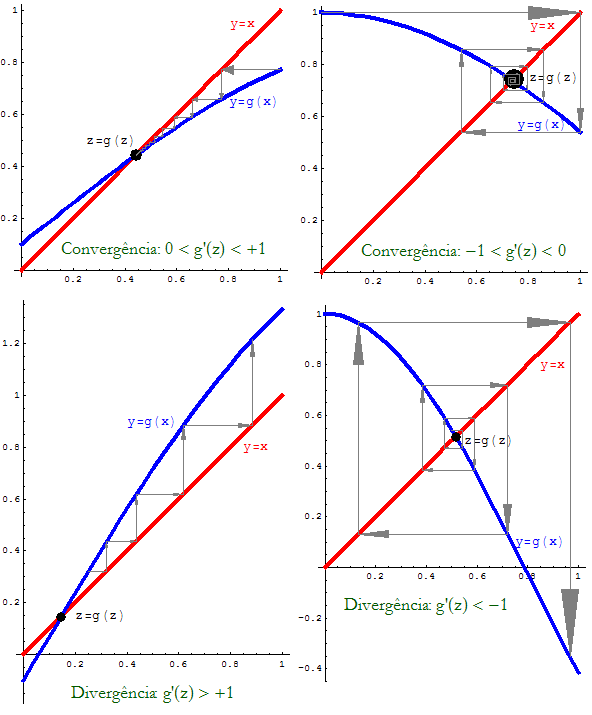
Figura 1: Casos do Método do Ponto Fixo. Nos dois casos de cima são apresentadas situações de convergência (monótona − à esquerda, alternada − à direita). O ponto fixo funciona como um atractor das iterações. Nos dois casos de baixo o ponto fixo actua como repulsor das iterações. Mesmo começando próximo do ponto fixo as iteradas divergem desse valor.

Definição:
Dizemos que uma função g é lipschitziana em [a, b] se existir um L > 0 tal que :

| g(x) − g(y) | < L | x − y | , ∀ x, y ∈ [a, b]

A função diz-se Contractiva se a constante de Lipschitz for inferior a um, ou seja quando L < 1.

Convém notar que as funções lipschitzianas são (absolutamente) contínuas no intervalo
(x→ y implicará imediatamente g(x)→ g(y)).
Quando a função é diferenciável, relacionamos esta noção com uma limitação da derivada.

Proposição:
Seja g ∈ C¹[a, b] tal que |g '(x)| ≤ L, ∀ x ∈ [a, b], então a função g é lipschitziana nesse intervalo, e quando L < 1 será contractiva.

dem:
Usando o T. Lagrange, para quaisquer x, y em [a,b], existe ξ ∈ ]x; y[ ⊂ [a, b] tal que

| g(x) − g(y) | = |g'(ξ)| |x-y| ≤ L |x − y|.

Nestas condições podemos apresentar o teorema do ponto fixo para a convergência num intervalo. Este teorema tem generalizações que se aplicam a sistemas de equações (e a equações funcionais).

Teorema (do ponto fixo num intervalo limitado).
Seja g uma função definida em [a, b] tal que:

g é contractiva em [a, b],
g é invariante em [a, b], ou seja g([a, b]) ⊆ [a, b] ,

então

g tem um e um só ponto fixo z ∈ [a,b] ;
qualquer que seja x₀ ∈ [a, b], a sucessão do método do ponto fixo, definida por x_n+1 = g(x_n) converge para z;
temos as seguintes estimativas de erro:
- (a posteriori)
  - (i) | e_n | < L | e_n-1 |
  - (ii) | e_n | < L/(1-L) | x_n − x_n-1|
- (a priori)
  - (iii) | e_n | < Lⁿ | e₀ |
  - (iv) | e_n | < Lⁿ (1-L)^-1 | x₁ − x₀ |
- Aqui L < 1 é a constante de contractividade.
  Quando g∈ C¹[a,b], L = max_{x∈ [a,b]} |g'(x)| < 1.

dem:

Existência (de ponto fixo no intervalo):
é uma consequência simples do teorema do valor intermédio.
Consideramos a função f(x)=g(x)-x. A invariância implica a≤ g(a), g(b)≤ b.
Assim f(a)f(b)≤ 0 e existe z∈ [a,b]: f(z)=0 ⇔ z=g(z).
Unicidade (de ponto fixo no intervalo)
Supondo z,w∈ [a,b] ambos pontos fixos, z=g(z) e w=g(w).
Temos pela contractividade
|z − w| = |g(z) − g(w)| ≤ L |z − w| ⇔ (1-L)|z − w|≤ 0
e como L < 1 temos |z − w|≤ 0 ou seja, z = w.
Convergência e estimativas:
Pela contractividade,
|e_n|=|z − x_n| = |g(z)-g(x_n-1)| ≤ L |z-x_n-1| = L |e_n-1|
obtemos a primeira estimativa que, aplicada repetidamente, dá-nos (iii)
|e_n| ≤ Lⁿ |e₀|.
Como L < 1 esta estimativa garante |e_n|→ 0 (notar que |e₀|≤ |a-b|), e conclui-se a convergência do método.
Finalmente (ii) resulta de
|e_n|≤ L|e_n-1| = L|z − x_n + x_n − x_n-1| ≤ L|e_n| + L|x_n − x_n-1|
logo (1 − L)|e_n| ≤ L|x_n − x_n-1| implica (ii).
Finalmente, (ii) implica |e₁| ≤ L/(1 − L) |x₁ − x₀| considerando n=1, e assim (iv) resulta de
|e_n| ≤ L^n-1 |e₁|.

Proposição:
Nas condições do Teorema do Ponto Fixo, temos ainda:

(a) Se 0 < g'(x) < 1, ∀ x ∈ [a, b] então a convergência é monótona
(as iterações ficam todas do mesmo lado face ao ponto fixo)
(b) Se -1 < g'(x) < 0, ∀ x ∈ [a, b] então a convergência é alternada
(as iterações alternam de lado face ao ponto fixo)

dem:
Como

e_n = g(z) − g(x_n-1) = g '(ξ_n) e_n-1

e como o sinal de g' é constante, por hipótese, temos

sign(e_n ) = sign( g '(ξ_n) ) sign(e_n-1 )

obtemos
no caso (a), sign(e_n ) = + sign(e_n-1 ) = ... = sign(e₀ ),
no caso (b), sign(e_n ) = − sign(e_n-1 ) = ... = (-1)ⁿ sign(e₀ ),
o que justifica a posição da iterada face ao ponto fixo.

Observação: Caso seja assegurada convergência alternada, temos z∈ [x_n-1; x_n]. Isto permite constituir novos intervalos onde sabemos estar o ponto fixo, e assim actualizar o valor de L.
Por exemplo, supondo que a derivada -1 < g' < 0 e é monótona, ao fim de p iterações podemos redefinir um novo

L_p = max { -g '(x_p-1); -g'(x_p) }

obtendo as estimativas seguintes com este novo valor. Uma possibilidade para uma nova estimativa a priori será

|e_p+k| ≤ (L_p)^k | x_p-1 − x_p |

Exemplo:
Um método para resolver equações quadráticas x²+bx-a=0 consiste em estabelecer a equivalência (para x≠ -b)

x²+bx-a=0 ⇔ x(x+b) = a ⇔ x = a/(x+b)

em que a função iteradora é g(x)=c/(x+1).
Isto leva a uma sucessão conhecida como fracção contínua

x_n+1 = a/(b+x_n) = a/(b + a/(b + a/(b + ...)))

que permite aproximar raízes quadradas com fracções, de uma forma optimal (para a grandeza dos valores).
Por exemplo, para a= b= 1, começando com x₀=1 obtemos

x₁=1/2, x₂=2/3, ..., x₆=13/21, ..., x₁₃=377/610, x₁₄=610/987, ...

o último valor x₁₄ = 610/987 = 0.6180344… é uma fracção de cálculo simples, que nos dá uma aproximação próxima do valor z=-1+√ 5=0.6180339887…
Podemos ver que no intervalo I=[1/2, 1] são verificadas as condições do teorema do ponto fixo:

contractividade: g'(x)=-(1+x)^-2 é crescente (g'' > 0) e negativa, logo
L = max_{x ∈ I} |g'(x)|= max{ -g'(1/2), -g'(1) } = max{ 4/9, 1/4} = 4/9 < 1
invariância: g é decrescente (g' < 0 ) e temos
g(1/2) = 2/3 ∈ [1/2,1], g(1) = 1/2 ∈ [1/2,1]

Isto justifica a convergência, que é alternada (g' < 0) sabendo-se logo que z∈ [377/610, 610/987] e para além disso, pelas estimativas a posteriori (i) e (ii) temos

|e₁₄| ≤ L/(1-L) |x₁₄-x₁₃| = 4/5×0.166…10^-5 < 0.133×10^-5

Como g' é crescente e negativa, considerando o intervalo reduzido

L₁₄= max {|g'(x₁₃)|, |g'(x₁₄)| } = 0.381966…

temos já uma estimativa muito precisa para as restantes iterações

|e_14+k|≤ 0.382^k (0.133×10^-5)

Teorema ("Divergência"):
Seja g∈ C¹(V_z) em que V_z é uma vizinhança do ponto fixo z.
Se | g '(z) | > 1, a sucessão do método do ponto fixo nunca converge para z, excepto se x_p=z (para alguma iterada p).

dem:
Como vimos, pelo T. Lagrange:

e_n+1 = g '(ξ_n) e_n

com ξ_n∈ [x_n;z] ⊂ V_z considerando x_n suficientemente próximo de z. Como | g '(z) | > 1, então numa vizinhança temos também | g '(ξ) | > 1, (pois g∈ C¹(V_z)).
Como e_n ≠ 0 (pois x_n≠ z)

|e_n+1| = |g '(ξ_n)| |e_n| > |e_n|

e o erro cresce, tornando impossível a convergência.

Este é um resultado local, que permite concluir a não convergência (... divergência) desde que se mostre que a derivada (em módulo) é maior que 1, num intervalo que contenha o ponto fixo.
Podemos estabelecer um resultado de convergência local, no outro caso. Este resultado é diferente do teorema do ponto fixo, pois não exige invariância, mas por outro lado temos que ter uma localização do ponto fixo, já que teremos que começar com uma iterada inicial suficientemente próxima desse valor.

Teorema (Convergência Local): Seja g∈ C¹(V_z) em que V_z é uma vizinhança do ponto fixo z.
Se | g '(z) | < 1, a sucessão do método do ponto fixo converge para z, quando x₀ for suficientemente próximo de z.

dem:
Podemos reduzir ao teorema do ponto fixo considerando

W_z = {x: |x − z| ≤ ε}

com ε pequeno tal que haja contractividade,

|g'(x)| < 1, ∀ x∈ W_z⊂ V_z ,

pois |g'(z)| < 1 e g∈ C¹(V_z). Assim, se x∈ W_z temos

|g(x) − z| = |g '(ξ)| |x − z | ≤ ε ⇐ g(x)∈ W_z

ficando demonstrada a invariância. Conclui-se pelo teorema do ponto fixo que há convergência, desde que x₀∈ W_z, ou seja, para valores iniciais suficientemente próximos de z.

Dentro das situações de convergência, há sucessões que convergem mais ou menos rapidamente, sendo conveniente distinguir a rapidez de convergência, introduzindo a noção de ordem de convergência.

Definição Seja (x_n) uma sucessão convergente para z.
Dizemos que (x_n) tem ordem de convergência p com coeficiente assimptótico de convergência K_p ≠ 0 se existir o limite

lim_n→∞

|e_n+1|

|e_n|^p

= K_p ≠ 0

Notamos que K₁≤ 1 porque se K₁ > 1 não poderia haver convergência: |e_n+1| > |e_n|.

Podemos distinguir 3 classes principais para a convergência:

SupraLinear (ou Exponencial): quando p>1 (ou p=1 e K₁ = 0).
Linear: p=1 e K₁ < 1
Logarítmica: p=1 e K₁ = 1

Há ainda as designações habituais de convergência quadrática quando p=2 e cúbica quando p=3 (não devem ser confundidas com designações semelhantes dadas noutro contexto, mais à frente no curso).
Convém ainda notar que se o limite for K_p=0 isso significa que a convergência é pelo menos de ordem p, mas deverá ser de ordem superior, devendo procurar-se o p correcto.

Exemplos:
Apresentamos alguns exemplos que ilustram esta definição, não estando necessariamente relacionados com o método do ponto fixo.
(i) Seja x_n = αⁿ com 0 < α < 1.
Esta sucessão converge para z=0, e temos

K₁ = lim_n→∞

|e_n+1|

|e_n|

= lim_n→∞

|αⁿ⁺¹|

|αⁿ|

= α ≠ 0

concluindo-se imediatamente a convergência linear com coeficiente assimptótico dado por K₁ = α.
(ii) Seja x_n = α^{β^n} com 0 < α < 1 < β.

[notar que x_n = α^(β^n) é diferente de (α^β)^n = α^(β n) ]

Esta sucessão também converge para z=0, mas temos

K₁ = lim_n→∞

|e_n+1|

|e_n|

= lim_n→∞

|α^{β^(n+1)}|

|α^{β^n}|

= lim_n→∞

|(α^{β^n})^β|

|α^{β^n}|

= lim_n→∞ (α^{β^n})^β-1 = 0

concluindo-se imediatamente que a convergência é supralinear (K₁ = 0), mas não identificamos a ordem exacta. Podemos verificar que

K_β = lim_n→∞

|e_n+1|

|e_n|^β

= lim_n→∞ (α^{β^n})^β-β = 1 ≠ 0

concluindo-se a ordem de convergência β > 1.
(iii) Finalmente um exemplo de convergência logarítmica.
Consideramos x_n = n^-b com b>0, que tende para z=0. Como,

K₁ = lim_n→∞

|e_n+1|

|e_n|

= lim_n→∞

|(n+1)^-b|

|n^-b|

= lim_n→∞ (1+1/n)^-b = 1^-b = 1

e conclui-se a convergência logarítmica.

Teorema (Ordem de Convergência − Método do Ponto Fixo):
Seja g∈ C^p(V_z) em que V_z é uma vizinhança do ponto fixo z.
Se g^(p)(z)≠ 0, e g'(z) = ... = g^(p-1)(z) = 0, então a ordem de convergência (local) do método do ponto fixo é p, e o coeficiente assimptótico é dado por

K_p = |g^(p)(z)| / p!

(notando que para p=1, devemos ter K₁ < 1 para assegurar a convergência local).

dem: A convergência local foi já assegurada no teorema anterior, quando K₁ = |g'(z)| < 1.
Pela expansão de Taylor com resto de Lagrange,

g(x_n) = g(z) + g^(p)(ξ_n)/p! (-e_n)^p, com ξ_n ∈ [x_n;z]

pois g'(z) = ... = g^(p-1)(z) = 0.
Por outro lado, g(x_n)=x_n+1 e z = g(z) implica

- e_n+1 = g^(p)(ξ_n)/p! (-e_n)^p,

Logo, substituindo em

K_p = lim_n→∞

|e_n+1|

|e_n|^p

= lim_n→∞ |g^(p)(ξ_n)|/p! = |g^(p)(z)| / p! ≠ 0

concluindo-se a ordem de convergência p.

Observação:
(i) É uma consequência imediata da definição de ordem de convergência que se um método tiver convergência de ordem p > 1, um método que consista em fazer duas iteradas terá ordem de convergência 2p. Dessa forma, o que é qualitativamente distinto é obter um método de convergência supra-linear, sendo relativamente secundária a ordem de convergência (ainda que esta seja mencionada com ênfase excessiva na literatura).
Por outro lado, note-se que se o método tiver convergência linear, duas iteradas apenas permitem reduzir o coeficiente assimptótico para metade. A distinção na convergência de métodos lineares é feita pelo coeficiente assimptótico e nos métodos supra-lineares é feita semelhantemente pela ordem de convergência.
(ii) Uma outra possibilidade para definição de ordem de convergência p, consiste em exigir que exista uma constante K_p > 0 tal que

|e_n+1| ≤ K_p |e_n|^p (n suficientemente grande)

(quando p=1 devemos ter K₁< 1), e não é necessário que exista um limite.
Para além disso, conhecendo a ordem de convergência, podemos estabelecer uma relação entre a diferença de iteradas e o erro absoluto:

|e_n| =

|x_n+1 − x_n|

|1 − e_n+1/e_n|

≤

|x_n+1 − x_n|

1 − K_p |e_n|^p-1

desde que K_p |e_n|^p-1 < 1, concluindo-se

|e_n| ≤

K_p |e_n-1|^p-1

1 − K_p |e_n-1|^p-1

|x_n − x_n-1|

... a expressão já era conhecida quando p=1 (a condição K₁ < 1 é a necessária para a convergência linear).

Com base na diferença de iteradas definimos um critério de paragem, notando que

|e_n| ≤

L_n

1 − L_n

|x_n − x_n-1|, quando L_n = K_p |e_n-1|^p-1 < 1

(o que acontecerá a partir de certa ordem, pois e_n → 0).

Método de Newton

O teorema anterior, acerca da ordem de convergência, permite-nos concluir convergência supralinear quando tivermos uma função iteradora cuja derivada seja nula no ponto fixo. Isso motiva procurar métodos que tenham essa característica.

Quando f '(x) ≠ 0 podemos estabelecer a equivalência

f(x) = 0 ⇔ x = x − f(x)/f '(x)

em que se define a função iteradora

g(x) = x − f(x)/f '(x),

e reparamos que na raiz z, como f(z)=0, obtemos

g'(x) = f(x) f ''(x)/(f '(x))² ⇒ g'(z) = 0

Assim, de acordo com o teorema anterior, a convergência com esta função iteradora será pelo menos quadrática, evitando o caso da derivada nula
(poderá até ser cúbica, caso f '(z) ≠ 0, f ''(z) = 0).

O Método de Newton consiste na aplicação do método do ponto fixo a g, isto é

Dado x₀ inicial;
Iterar

x_n+1 = x_n − f(x_n)/f '(x_n)
.

e como vimos, exceptuando o caso f '(z)=0, asseguramos uma convergência local pelo menos quadrática.

Observações:
(1) O método de Newton tem uma interpretação geométrica que está na origem da sua dedução inicial, conforme a Figura 2.

Figura 2: Iterações no método de Newton. Começando com x₀=1, o novo ponto x₁ resulta da intersecção da recta tangente com a recta y=0, e assim sucessivamente.

Geometricamente, a ideia consiste em usar a recta tangente

y = f(x_n) + f '(x_n)(x-x_n)

como aproximação da função f em x_n (é a aproximação de primeira ordem, na expansão de Taylor). Deduzindo o valor x tal que y=0 obtemos a mesma expressão

0 = f(x_n) + f '(x_n)(x-x_n) ⇔ x = x_n − f(x_n)/f '(x_n)

e esse valor x constitui a nova aproximação x_n+1.

(2) Podem deduzir-se aproximações superiores considerando expansões de Taylor de ordem superior. Aumenta-se a ordem de convergência, mas perde-se em eficácia computacional.
É importante realçar que n-iterações do método de Newton são normalmente mais eficazes do que uma iteração de outro método de ordem 2n.

Exemplos:
Podemos ver alguns exemplos que ilustram a rapidez de convergência do Método de Newton (também denominado Newton-Raphson).
(i) Calcular z= ^p√ a usando apenas simples operações aritméticas.
Neste caso, z é solução de f(x) = x^p − a = 0.
De acordo com o teorema de convergência local, para um x₀ suficientemente próximo, o método fica

x_n+1 = x_n − (x_n^p-a)/(p x_n^p-1) = x_n(1-1/p) + (a/p) x_n^1-p

e ainda fica mais simples no caso do cálculo de raízes quadradas (p=2)

x_n+1 = x_n/2 + a/(2 x_n)

(especialmente trabalhando em sistema binário, onde as divisões/multiplicações por 2 são imediatas).
(ii) Vejamos por exemplo o cálculo de z= ³√ 6:

x₀ = 2, x₁ = 11/6, x₂ = 1.817263…, x₃ = 1.81712060…, x₄ = 1.817120592832139…

e nesta quarta iterada os dígitos apresentados são já os correctos.
(iii) Recuperando o exemplo da fracção contínua, a aplicação do método de Newton a f(x)=x²+bx-a=0 leva a cálculos que envolvem fracções também simples

x_n+1 = x_n − ((x_n+b)x_n-a)/(2x_n+b) = (x_n²+a)/(2x_n+b)

obtendo-se para x₀=1

x₁=2/3, x₂=13/21, x₃=610/987, x₄=1346269/2178309, ...

reparando se tratam de valores também obtidos na fracção contínua, mas muito mais rapidamente (aqui a 2ªiterada é a 6ª iteração da fracção contínua, a 3ª é a anterior 14ª, e a 4ª seria a 30ª). A fracção x₄ apresenta já um erro inferior a 10^-13.

Mais uma vez, interessa estabelecer condições suficientes que assegurem uma convergência não apenas local − para uma iterada inicial "suficientemente próxima" − mas sim para um conjunto alargado de iteradas iniciais − num intervalo.

Teorema (Condições Suficientes de Convergência − Método de Newton):
Seja f∈ C²[a,b] tal que nesse intervalo

(1) f(a) f(b) ≤ 0 ;
(2) f ' (x) > 0 ou f ' (x) < 0 ;
(3) f '' (x) ≥ 0 ou f '' (x) ≤ 0 ;

Então o Método de Newton tem convergência (pelo menos) quadrática para a solução única
z ∈ [a,b], inicializando o método:

(a) com x₀∈ [a,b] : f(x₀) f ''(x) ≥ 0
(b) com qualquer x₀∈ [a,b] se |f(a)/f '(a)|, |f(b)/f '(b)| ≤ |b − a|

dem:
A demonstração mais simples não é construtiva, pelo que a omitimos.

Notamos que as condições 1) e 2) implicam a existência e unicidade de solução (pelo T. valor Intermédio e T. Rolle).
A condição 3) é importante para evitar uma mudança de concavidade, que pode levar a uma situação cíclica, não convergente:
− Por exemplo, se f(x) = x³ − 5 x, em [-1,1] há um único zero (que é z=0) e as condições 1) e 2) são verificadas, mas não a condição 3), pois f ''(x)=6x muda de sinal em [-1,1]. De facto, podemos ver que
x₀ = 1, x₁ = 1 − (1-5)/(3-5) = -1, x₂ = 1, ..., x_k = (-1)^k,
e a sucessão definida pelo Método de Newton não converge!
Finalmente, observamos que a condição a) é sempre verificada por um dos extremos do intervalo, mas para assegurar a convergência para qualquer iterada inicial x₀, a condição exigida em b) garante que as iteradas, mesmo começando nos extremos, não saiem do intervalo... por exemplo, se x₀=a
x₁ = a − f(a)/f '(a) ⇐ |x₁ − a| = |f(a)/f '(a)| ≤ |b − a|
Podemos ver ainda que a convergência é monótona para as iteradas iniciais que verifiquem (a). Mais, a condição (b) só precisa de ser verificada para o extremo que não verifica (a) ficando x₁ nas condições de (a), ou seja, a convergência será monótona a partir daí.

Teorema (Estimativas de Erro − Método de Newton):
Seja f∈ C²[a,b] nas condições de convergência anteriores. Temos a seguinte fórmula de erro:

∃ ξ ∈ [x_n; z] : e_n+1 = −

f ''(ξ)

2 f '(x_n)

(e_n)²

resultando no coeficiente assimptótico

K₂ =

|f ''(z)|

2 |f '(z)|

e nas estimativas

(a posteriori)

|e_n| ≤ max_{x∈ [a,b]} |f ''(x)|
2 |f '(x_n-1)| |e_n-1|²
(a priori)
M |e_n| ≤ (M|e₀|)^{2^n}
onde
M = max_{x∈ [a,b]} |f ''(x)|
2 min_{x∈ [a,b]}|f '(x)|

dem:
− A fórmula de erro resulta da aplicação da expansão de Taylor

0 = f(z) = f(x_n) + f '(x_n)(z-x_n) + ½f ''(ξ_n)(-e_n)²

dividindo por f '(x_n)≠ 0 obtemos

0 = f(x_n)/f '(x_n) + z − x_n + ½f ''(ξ_n)/f '(x_n)(e_n)²

e como f(x_n)/f '(x_n) − x_n = -x_n+1 obtemos a fórmula de erro,

0 = z − x_n+1 + ½f ''(ξ_n)/f '(x_n)(e_n)²

Como ξ ∈ [x_n; z] e x_n → z obtém-se K₂ pela divisão de |e_n+1| por |e_n|². Finalmente
− a 1ª estimativa resulta directamente, pois ξ ∈ [x_n; z]⊂ [a,b].
− a 2ª estimativa resulta ainda directamente pois

M |e_n| ≤ (M|e_n-1|)²

bastando aplicar consecutivamente.

Observações:
(i) Quando f '(z)=0 estamos numa situação de raiz (pelo menos) dupla, e o método de Newton perde a convergência quadrática, sendo possível uma pequena modificação para recuperar essa convergência (ver e.g. [CA]).
(ii) Quando f ''(z)=0 (e f'(z) ≠ 0) obtemos uma ordem de convergência superior à quadrática, que será cúbica. Conforme já referido, ainda que melhor, não é qualitativamente superior − são ambas convergências supra-lineares.
Como regra empírica se a convergência quadrática significa uma {em duplicação do número de dígitos exactos} em cada iterada, a convergência cúbica significará uma triplicação. Na prática isso significa que na zona de convergência a precisão dupla é alcançada em menos de 4 ou 5 iterações, pelo que é mais importante conseguir uma boa aproximação inicial.
(iii) Reforçando este ponto, resulta das estimativas de erro que para obter uma estimativa a priori aceitável o valor M|e₀| deve ser inferior a 1, e isso significa que a iterada inicial não deve estar afastada da raiz (tanto menos quanto os valores de |f '| forem pequenos ou os valores de |f ''| forem grandes).

Exemplo:
Consideremos f(x)= e^-x − log(x) = 0, que verifica no intervalo [1,2]:

1) f(1) = e^-1 > 0, f(2) = e^-2-log(2) < 0;
2) f '(x) = -e^-x-1/x < 0 (para x∈ [1,2])
3) f ''(x) = e^-x+1/x² > 0 (para x∈ [1,2])

estão reunidas as condições suficientes para a convergência quadrática do Método de Newton, pelo menos para iteradas iniciais: f(x₀)>0 [conclusão (a) do Teorema], como é o caso x₀=1.
Como |f(1)/f '(1)| = 0.2689… , |f(2)/f '(2)| = 0.87798… < |2-1| = 1 concluímos que essa convergência ocorre para qualquer x₀∈ [1,2].
Começando com x₀=1 obtemos

x₁=1.2689…, x₂=1.309108…, x₃=1.3097993887…

como |f(x₃)|≤ 2.04× 10^-7 e min_[1,2]|f '|=|f '(2)| > 0.635, a estimativa geral a posteriori dá-nos

|e₃|≤ 2.04× 10^-7 / 0.635 < 3.21× 10^-7.

e constata-se que x₃ tem já 7 dígitos correctos.
Podemos prever o comportamento seguinte com esta informação.
Usando um intervalo tão pequeno podemos considerar M≈ K₂ ≈ 0.413, logo

0.412|e_k+3| ≤ (M|e₃|)^{2^k} ≤ (1.325× 10^-7)^{2^k}

o que significa que x₅=1.30979958580415… apresentará já um erro

|e₅|≤ 0.412^-1(1.325× 10^-7)⁴ < 10^-27

tornando-se completamente inúteis outras iterações em precisão dupla, pois a precisão fica completamente esgotada, restando o inevitável erro de arredondamento.

Método da Secante

O método da Secante é uma variante do método de Newton, que evita o cálculo de derivadas, substituindo-as pelo cálculo duma razão incremental (que no limite coincidirá com a própria derivada).

O método tem uma dedução geométrica semelhante à do método de Newton.
Dados dois pontos x_n-1 e x_n podemos definir a recta "secante" que passa pelas suas imagens:

y = f(x_n) +

f(x_n) − f(x_n-1)

x_n − x_n-1

(x − x_n)

em que a derivada é agora substituída pela razão incremental.
De forma semelhante, resolvendo y=0 obtemos

x = x_n −

x_n − x_n-1

f(x_n) − f(x_n-1)

f(x_n)

que será o valor para a nova aproximação x_n+1.

Resumindo, o Método da Secante consiste em

Definir duas iteradas iniciais x_-1 e x₀.
Iterar

x_n+1 = x_n − x_n − x_n-1
f(x_n) − f(x_n-1) f(x_n)

Observação: Reparamos que, em cada iteração, não é necessário calcular duas vezes a função f, pois o valor f(x_n-1) deve ficar armazenado na iteração anterior. Desta forma o método é computacionalmente mais eficaz que o método de Newton (na maioria dos casos), que exige também o cálculo actualizado da derivada.

Fórmula do Erro (Método da Secante)
Não entrando em detalhes, é possível estabelecer a seguinte expressão do erro

∃ ξ_n, η_n ∈ [x_n-1; x_n; z] : e_n+1 = −

f ''(ξ_n)

2 f '(η_n)

e_n e_n-1

Esta fórmula permite obter estimativas de erro na forma

|e_n+1| ≤

max |f ''(x)|

2 min |f '(x)|

|e_n| |e_n-1|

e ainda concluir acerca da ordem de convergência do método.
A convergência será supralinear, quando f '(z) ≠ 0, pois

lim_n→∞

|e_n+1|

|e_n|

= lim_n→∞

|f ''(ξ_n)|

2 |f '(η_n)|

|e_n-1| =

|f ''(z)|

2 |f '(z)|

lim_n→∞ |e_n-1| = 0

já que |e_n|→ 0 (assumindo a convergência).
Pode demonstrar-se (e.g. [KA]) que se f '(z) ≠ 0 a ordem de convergência do método da Secante será p=(1+√ 5)/2 = 1.618… o número de ouro.

NOTA: De facto, sendo y_n = log|e_n| podemos estabelecer, formalmente, aplicando logaritmos à fórmula do erro, uma relação limite y_n+1 ≈ C + y_n + y_n-1 que é uma sucessão de Fibonacci, e da razão y_n+1/y_n → p obtemos log|e_n+1|≈ p log|e_n|, o que é uma justificação simples para esse valor p.

Teorema (Condições suficientes de convergência − Método da Secante)
Seja f ∈ C²[a,b]. Nas condições (1), (2), (3), do Teorema para o Método de Newton, o método da Secante converge supralinearmente (com ordem p = 1.618…), inicializando

(a) com x_-1, x₀ ∈ [a,b] : f(x_-1)f ''(x) ≥ 0 , f(x₀)f ''(x) ≥ 0
(b) com quaisquer x_-1, x₀ ∈ [a,b] se |f(a)/f '(a)|, |f(b)/f '(b)| ≤ |b − a|

Exemplo:
Consideremos de novo f(x)= e^-x-log(x) = 0 as condições (1), (2), (3) foram já verificadas no intervalo [1,2]. Como também se verificava (b), podemos usar qualquer par de iteradas iniciais, concluindo-se a convergência supralinear do método da Secante.
Começando com x_-1=1, x₀=1.5, obtemos

x₅=1.309799585804… com |e₅|≤ |f(x₅)|/0.635 < 2× 10^-13

(usando a estimativa geral a priori) sendo apenas necessário calcular mais uma iteração para esgotar a precisão dupla.

Bibliografia citada

[CA] C. J. S. Alves, Fundamentos de Análise Numérica (I), Secção de Folhas AEIST (2002).
[KA] K. Atkinson: An Introduction to Numerical Analysis, Wiley (1989)

[Capítulo 1] [Capítulo 2] [Capítulo 3] [Capítulo 4] [Capítulo 5]

C J S Alves (2008, 2009)

Matemática Computacional Resumo da matéria [Versão 3.1]

Capítulo II Métodos para Equações não Lineares

Localização de Raízes

Método da Bissecção

Método do Ponto Fixo

Método de Newton

Método da Secante

Matemática Computacional

Resumo da matéria [Versão 3.1]

Capítulo II

Métodos para Equações não Lineares