O integral (continuação).
Funções dadas por integrais indefinidos.
Aplicação do integral ao cálculo de áreas.
Material de estudo:
Na aula anterior introduzimos a função conhecida como o integral indefinido de uma função \(f(x)\), \(\varphi_a\) ou, simplesmente, \(\varphi\): para \(f\) definida num intervalo \(D\), integrável em cada intervalo limitado contido em \(D\), define-se o integral indefinido \[\varphi(x)=\int_a^x f(t)\,dt.\] Vimos que esta função tem as seguintes propriedades:
A última expressão também se pode escrever, \[\left(\int_a^xf(t)\,dt\right)'=f(x).\] Ou seja, se \(f\) é contínua num intervalo \(D\) e \(a\in D\), então o integral indefinido \(F_a\) é uma primitiva de \(f\) em \(D\).
Uma função pode ser dada como sendo o integral indefinido de uma determinada função. Um exemplo importante foi já mencionado na aula anterior: a função erro usado na estatística: \(\operatorname{erf}(x)=\frac{1}{\sqrt{2\pi}}\int_0^x e^{-x^2}.\) Esta função, em particular não tem representação em termos das funções elementares que conhecem.
Referimos aqui que a própria função logaritmo poderia ter sido dada como o integral indefinido \[\ln x=\int_1^x \frac{1}{t}\,dt,\quad\text{para}\quad x>0.\]
Portanto, dada uma função usando o integral indefinido vamos querer estudá-la e, portanto, calcular os seus intervalos de monotonia e extremos, concavidades e assíntotas, como qualquer outra função.
Damos em seguida alguns exemplos de cálculo da derivada de funções envolvendo o integral indefinido \(\varphi(x):\)
Exemplo 1. seja \(f(x)=e^{-x^2}\). Pelo TFC, podemos dizer que se \[\varphi(x)=\int_0^x e^{-t^2}\,dt\qquad \text{então}\qquad \varphi'(x)=e^{-x^2},\quad \forall x.\]
Exemplo 2. \(F(x)=\displaystyle\int_x^{-1}\frac{e^t}{t}dt\quad\) tem domínio \(D=\mathbb{R}^-\). Relembre que \(f(t)=\dfrac{e^t}{t}\) é contínua quer em
\(\;\mathbb{R}^-,\;\) quer em \(\;\mathbb{R}^+\), mas o ponto inicial \(-1\in \mathbb{R}^-.\quad\) Assim, se fosse \(\;x\gt 0\;\) o intervalo de integração seria \([-1,x]\) o que
incluiria o zero, e a função integranda não seria limitada e portanto não integrável nesse intervalo o que é absurdo.
Temos então,
\[F'(x)=\left(\int_x^{-1}\frac{e^t}{t}\right)'=\left(-\int_{-1}^x\frac{e^t}{t}\right)'=-\frac{e^x}{x},\qquad x\lt 0.\]
Exemplo 3. \(G(x)=\displaystyle\int_2^{x^2}\frac{e^t}{t}dt\quad\) tem domínio \(D=\mathbb{R}\setminus\{0\}\).
Temos que olhar para a função \(G\) como a função \(\varphi(b(x))\) composta do integral indefinido \(\varphi(x)=\int_2^x \frac{e^t}{t}\,dt\) com \(b(x)=x^2\).
Como \(f(t)=\dfrac{e^t}{t}\) é contínua em \(\mathbb{R}^+\) então é contínua no intervalo fechado entre \(2\) e \(x^2\)e, logo, \(\varphi'(x)=f(x).\)
Usando o teorema da derivada da função composta,
\[G'(x)=\left(\varphi(b(x))\right)'=f(b(x))b'(x)=\frac{e^{x^2}}{x^2}2x=\frac{2e^{x^2}}{x}.\]
Exemplo 4. \(\displaystyle G(x)=\int_x^{x^2}\frac{e^t}{t}dt,\qquad\) tem domínio \(D=\mathbb{R}^+\).
Para derivar \(G\) escrevemos,
\[G(x)=\int_x^a \frac{e^t}{t}dt+\int_a^{x^2} \frac{e^t}{t}dt=-\int_a^x \frac{e^t}{t}dt+\int_a^{x^2} \frac{e^t}{t}dt.\]
Logo, usando o exemplo 3,
\[G'(x)=-\frac{e^x}{x}+\frac{2e^{x^2}}{x}.\]
Os exemplos 2, 3 e 4 são casos particulares do seguinte resultado:
Se \(a(x)\) e \(b(x)\) são diferenciáveis e \(f\) é contínua, então, \[\left(\int_{a(x)}^{b(x)}f(t)\,dt\right)'=b'(x)f(b(x))-a'(x)f(a(x)).\]Resulta de considerar o integral indefinido de \(f\), \(\varphi(x)=\int_c^xf(t)\,dt\;\) \(c\) fixo, e escrever, \[\left(\int_{a(x)}^{b(x)}f(t)\,dt\right)'=\left(\int_{c}^{b(x)}f(t)\,dt-\int_{c}^{a(x)}f(t)\,dt\right)' =\left(\varphi(b(x))-\varphi(a(x))\right)'\] e o resultado sai do TFC e da regra de derivação da função composta.
Pode ainda dar-se o caso da expressão integranda envolver \(x\) como no exemplo seguinte
Exemplo 5. \(\displaystyle G(x)=\int_1^{x}\frac{x^2e^t}{t}dt,\quad\) tem domínio \(\mathbb{R}^+\).
Como \(x\) é independente de \(t\), tratamo-lo como uma constante a multiplicar a função integranda. Logo,
\[\left(\int_1^{x}\frac{x^2e^t}{t}dt\right)'=\left(x^2\int_1^{x}\frac{e^t}{t}dt\right)'=2x\int_1^{x}\frac{e^t}{t}dt+x^2\cdot\frac{e^x}{x}.\]
Observação O Teorema Fundamental do Cálculo estabelece a ligação entre o Cálculo Diferencial (derivadas) e o Cálculo Integral (integrais). À partida nada nos fazia suspeitar que o conceito de derivada e portanto de primitiva, estivesse relacionado com o conceito de integral. Relembremos as interpretações geométricas aparentemente não relacionadas da derivada e do integral.
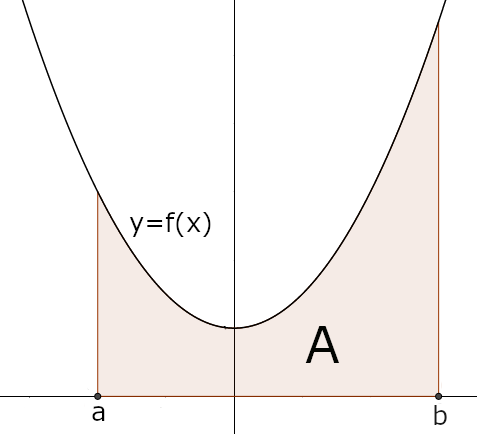
Definição (Área - I)Por vezes, designamos aquele conjunto \(A\) por \(A_f(a,b)\) quando for preciso dizer qual a função e o intervalo considerados.Seja \(f(x)\geqslant 0\), para todo \(x\in[a,b].\quad\) Seja \(A\) o conjunto do plano \(Oxy\) dada por \[A=\{(x,y)\;:\;0\leqslant y\leqslant f(x)\;\wedge \; a \leqslant x \leqslant b\}.\] Define-se a área do conjunto \(A\) como sendo \[\operatorname{Área}(A)=\int_a^b f(x)\,dx,\] se este integral existir.

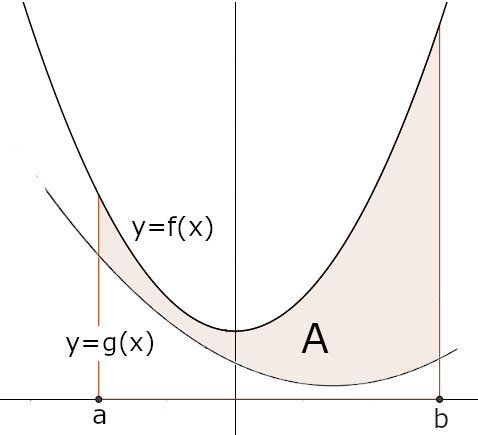
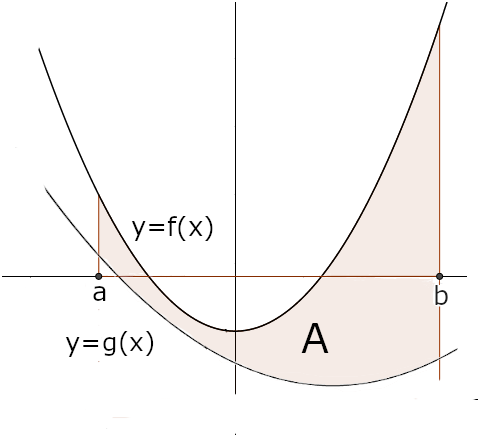
Definição (Área - II)Sejam \(f, g\) limitadas tais que, \(g(x)\leqslant f(x)\), para todo \(x\in[a,b].\quad\) Seja \(A\) o conjunto do plano \(Oxy\) dada por \[A=\{(x,y)\;:\;g(x)\leqslant y\leqslant f(x)\;\wedge \; a \leqslant x \leqslant b\}.\] Define-se a área do conjunto \(A\) como sendo \[\operatorname{Área}(A)=\int_a^b \left(f(x)-g(x)\right)\,dx,\] se este integral existir.
Assumindo que \(f,g\) são contínuas, podemos usar a regra de Barrow e calcular a área de regiões bastante gerais.
A seguinte ferramenta do GeoGebra permite visualizar a região \(A\) e calcular a respeciva área. Nos campos adequados pode introduzir as funções \(f(x)\) e \(g(x)\) e, com os cursores, escolher os valores de \(a\) e \(b\).