Aula teórica 27 - 2ª parte

O integral.
Motivação da definição: "área debaixo do gráfico".
Propriedades básicas do integral.

Aula teórica 28

Material de estudo:

• [AB] A. Bastos e A. Bravo, Cálculo Diferencial e Integral I. Texto de apoio às aulas, 2010.,   Cálculo Diferencial e Integral I. Texto de apoio às aulas, páginas 108-115,.
• [I] Exercícios resolvidos:  Integral: definição e propriedades. - Exercícios 1 - 4.
• [CF] J. Campos Ferreira. Introdução à Análise Matemática, Fundação Gulbenkian, 8a ed., 2005.
  

Juntamente com os de limite, de continuidade e de derivada, o de integral é um dos quatro conceitos mais importantes desta disciplina.
Vamos introduzir a noção de integral de uma função limitada começando com uma motivação baseada na interpretação deste como a área de uma região do plano limitada entre o eixo das abcissas e o gráfico da função (no caso de uma função positiva).

Numa primeira fase, não nos ocuparemos da definição rigorosa do integral nem de condições específicas que garantam a sua existência. Em vez disso, veremos como, com base na interpretação do integral como área e nas propriedades da área de conjuntos no plano, resultam naturalmente as propriedades que conduzem a um dos mais importantes resultados do Cálculo: O Teorema Fundamental do Cálculo. É este o resultado que estabelece a relação entre o integral e as primitivas, sendo, por isso o elo de ligação entre o Cálculo Integral e o Cálculo Diferencial, proporcionando um método prático de cálculo de integrais.

Numa aula posterior procederemos à definição do integral e veremos de que forma os resultados deste guia de estudo podem ser obtidos a partir dessa definição. Nessa altura também se estudarão algumas condições que garantam a existência do integral.

O integral (início)

Motivação: "área debaixo do gráfico".

Seja \(f\) uma função limitada (isto é, minorada e majorada) definida num intervalo \(\;I=\left[a,b\right]\;\) com \(a\lt b\) finitos.

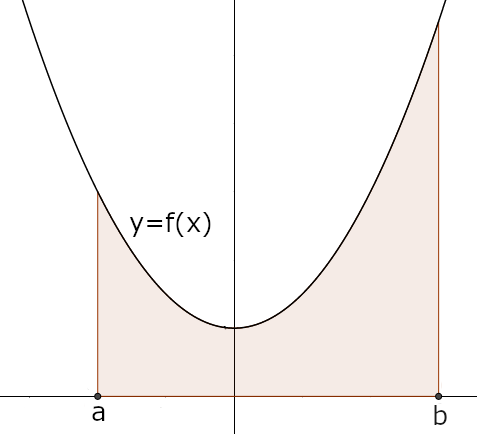
Vamos, numa primeira abordagem, simplificar a interpretação geométrica considerando \(f\) não negativa,isto é, \(\;f(x)\geqslant 0\;\), para todo \(\;x\in I.\). Consideremos o seguinte subconjunto do plano \(0xy\): \[A=\{(x,y)\;:\;0\leqslant y\leqslant f(x)\;\wedge \; a \leqslant x \leqslant b\}.\]

Por outras palavras, \(A\) é a região do plano compreendida entre o eixo das abcissas \(0x\) e o gráfico da função \(f\) para \(x\) entre \(a\) e \(b\). Veja o exemplo na figura em baixo em que \(A\) é a região colorida:

O integral de \(f\) no intervalo \(\;[a,b]\;\) o qual representaremos por \[\int_a^b f(x)\,dx\]

Esta caracterização está longe de ser rigorosa e veremos, que, quando a função \(f(x)\) não é contínua, em muitas situações o próprio conceito de área da região \(A\) poderá não ser claro e o integral poderá não existir. Sempre que o integral exista em \([a,b]\), independentemente da continuidade de \(f\), dizemos que \(f\) é integrável em \([a,b]\). A questão da existência do integral será abordada noutra aula depois de definido o integral de forma rigorosa.

Exemplo 1. \(\;f(x)=c\) constante. O conjunto \(A\) será o rectângulo \(\;[a,b]\times [0,c]\;\) e, portanto, a sua área será dada por \[\int_a^b c\,dx=(b-a)c.\] É claro que se a constante \(c\) for nula, teremos, \[\int_a^b 0\,dx=0.\] (A área de uma linha é zero).

Exemplo 2. \(\;f(x)=x\) num intervalo \([0,b],\) com \(b\gt 0.\) Neste caso, o conjunto \(A\) é um triângulo rectângulo de base \(b\) e altura \(b,\) cuja área é dada por, \[\int_0^b x\,dx=\frac{b^2}{2}.\]

Exemplo 3. \(\;f(x)=\sqrt{r^2-x^2}\;\) no intervalo \([-r,r]\;\) para \(r\gt 0.\;\) A curva \(y=f(x)\) é a semicircunferência superior centrada em \(0\) e de raio \(r\). O conjunto \(A\) será então um semicírculo de raio \(r\) cuja área é, \[\int_{-r}^r \sqrt{r^2-x^2}\,dx=\frac{\pi r^2}{2}.\]

É claro que, no caso geral, precisamos de um método analítico que nos permita calcular integrais, incluindo os anteriores, que seja independente de interpretações geométricas. Aliás, o processo irá ser exactamente o inverso do sugerido nos exemplos anteriores: com base nos resultados analíticos obtidos a partir do Teorema Fundamental do Cálculo, é que iremos calcular as áreas de conjuntos. Para isso, teremos que considerar a definição do integral, o que irá ser feito numa aula posterior e que será baseada na aproximação do conjunto \(A\) por rectângulos.

Propriedades básicas do integral.

Para já, vamo-nos servir das propriedades intuitivas da área para prevermos (o que não é o mesmo que "deduzir") quais serão as propriedades básicas que o integral terá que possuir.

Essas propriedades são:

• A área de um subconjunto do plano não varia para translações desse conjunto (invariância da área para translações),
• A área da união de dois conjuntos de pontos no plano é igual à soma das áreas de cada um dos conjuntos individuais (propriedade aditiva da àrea),
• A área é proporcional a rescalamentos na direção vertical, isto é, multiplicando a ordenada de todos os pontos do conjunto por uma constante \(c>0\) a área do conjunto resultante é \(c\) vezes a área do conjunto original (propriedade do rescalamento da área).

Estas propriedades traduzidas para os integrais correspondem às seguinte quatro propriedades elementares, as quais de momento ficam inituitivamnente justificadas para funções \(f,g\) e constante \(k\) não negativas:

1. \(\displaystyle\int_a^b (f(x)+g(x))\,dx=\int_a^b f(x)\,dx+\int_a^bg(x)\,dx,\)
2. \(\displaystyle\int_a^b kf(x)\,dx=k\int_a^bf(x)\,dx,\)
3. \(\displaystyle\int_a^cf(x)\,dx+\int_c^bf(x)\,dx=\int_a^bf(x)\,dx,\;\) para \(\;a\lt c\lt b.\)

E se a função \(f(x)\) não for necessariamente não negativa, qual será o significado do seu integral?

A generalização do integral para esta situação é feita de forma a que as propriedades 1.-3. anteriores continuem válidas, com \(f,g\) e \(k\) podendo tomar valores negativos.

Consideremos, em primeiro lugar, o caso \(f(x)\leqslant 0,\) para todo \(x\in [a,b].\;\) Nesse caso, para que seja satisfeita a propriedade 2. teremos, \[\int_a^b f(x)\,dx=\int_a^b(-1)\cdot |f(x)|\,dx=-\int_a^b |f(x)|\,dx.\]

Isto significa que, neste caso, \(\;\int_a^b f(x)\,dx\;\) é o simétrico da área do conjunto compreendido entre o gráfico de \(|f|\) e o eixo das abcissas, no intervalo \([a,b].\;\) Esta àrea coincide com a área do conjunto compreendido entre o gráfico de \(f(x)\) e o eixo das abcissas.

Observação importante: a área é sempre uma quantidade positiva ou nula, independentemente da posição do conjunto no plano. Aliás, usando a invariãncia para translações, podemos sempre reduzir o problema o cálculo da área de um conjunto qualquer ao cálculo da área de um conjunto no semiplano superior.

Para o caso mais geral, considere, por exemplo, a função esboçada na figura seguinte:

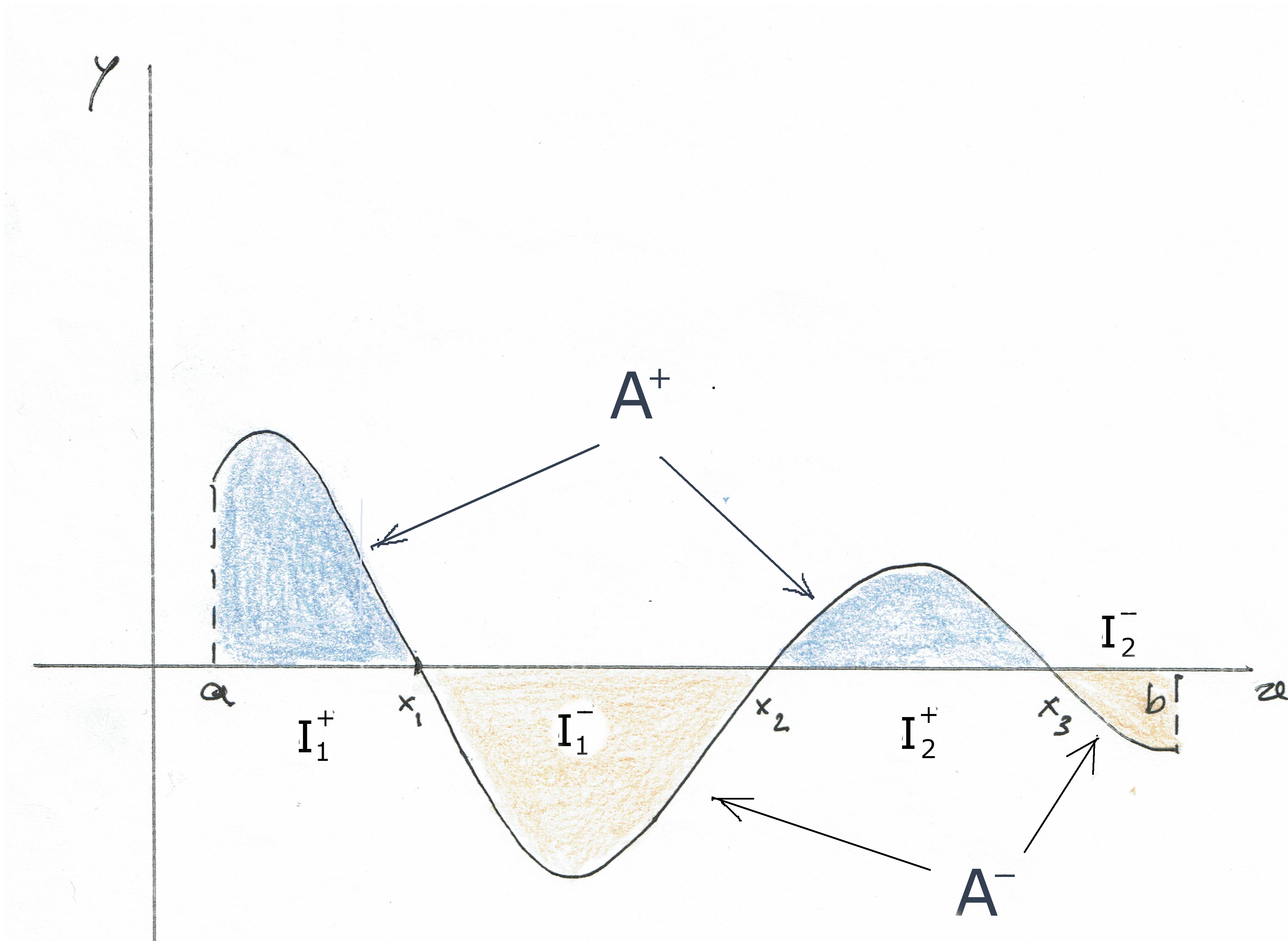
Então, reportando-nos à figura, pela propriedade 3. teremos, \[\begin{aligned}\int_a^bf(x)\,dx&=\int_a^{x_1} f(x)\,dx+\int_{x_1}^{x_2} f(x)\,dx+\int_{x_2}^{x_3} f(x),dx+\int_{x_3}^{b} f(x)\,dx\\ &=\left(\int_a^{x_1} f(x)\,dx+\int_{x_2}^{x_3} f(x)\,dx\right)-\left(\int_{x_1}^{x_2} |f(x)|\,dx+\int_{x_3}^{b} |f(x)|\,dx\right)\\ &=\text{Área de }A^+-\text{Área de }A^-. \end{aligned}\]

Seja \(\;[a,b]=I^+\cup I^-\;\) de tal modo que, \(\;f(x)\geqslant 0,\;\) para \(\;x\in I^+,\;\) e \(\; f(x)\leqslant 0,\;\) para \(\;x\in I^-.\;\) Então, se, \[A^+=\{(x,y) : x\in I^+ \wedge\; 0\leqslant y\leqslant f(x)\}\quad\text { e }\quad A^-=\{(x,y) : x\in I^- \wedge\; f(x)\leqslant y\leqslant 0\},\] teremos, \[\int_a^bf(x)\,dx=\text{Área de }A^+ - \text{Área de }A^-.\]

Exemplo 4. \[\int_0^3 (6x-12)\,dx= 6\int_0^3 x\,dx-\int_0^3 12\,dx=6\cdot\frac{9}{2}- 12\cdot 3=27-36=-9.\] Exercício: veja que \(\;I^+=[2,3],\;\) \(\,I^-=[0,2],\;\) identifique \(\;A^+,\,A^-\;\) (neste caso são triângulos rectângulos), e interprete este resultado numérico em termos das áreas de \(A^-\) e \(A^+\).

Exemplo 5. \[\int_{-\pi}^{\pi}\operatorname{sen}x\,dx=0,\] dado que, sendo \(\;\operatorname{sen}x\;\) uma função ímpar (isto é, \(\operatorname{sen}(-x)=-\operatorname{sen} x\)) e os extremos de integração simétricos, os conjuntos \(A^+\) e \(A^-\) têm igual área.

O Teorema da média

Definição (valor médio de uma função).

Dada \(f\) integrável em \([a,b]\), define-se o valor médio de \(f\) em \([a,b]\): \[\bar{f}=\frac{1}{b-a}\int_a^b f(x)\,dx.\]

Exemplo 6. Usando a interpretação geométrica do integral facilmente se conclui que, dados \(a\lt b\) se tem \[\int_a^b x\,dx=\frac{b^2}{2}-\frac{a^2}{2}.\] Temos então, que em \([a,b]\), a média da função \(f(x)=x\) é dada por \[\bar{f}=\frac{1}{b-a}\int_a^b x\,dx=\frac{b^2-a^2}{2(b-a)}=\frac{a+b}{2}.\]

Teorema (da média para funções contínuas)

Seja \(f\) uma função contínua em \(\;[a,b]\;\) com \(a\lt b\) finitos. Então, existe \(c\in\left]a,b\right[\) tal que \[\bar{f}=f(c)\]

Por outras palavras, o valor médio da função \(f\) em \([a,b]\) é assumido por \(f\) em algum ponto interior do intervalo \([a,b]\). Veja o caso do Exemplo 6.

A igualdade \[\frac{1}{b-a}\int_a^b f(x)\,dx=f(c)\] para algum \(c\in\left]a,b\right[\) vai ser de crucial importância para a obtenção do Teorema Fundamental do Cálculo.

É claro que, de momento não podemos ainda demonstrar este resultado uma vez que ainda não definimos rigorosamente o integral. No entanto, a sua interpretação geométrica é muito clara, pelo menos no caso de função \(f(x)\) não negativa: dizer que existe \(c\in\left]a,b\right[\) tal que \[\int_a^bf(x)\,dx=f(c)(b-a),\] equivale a dizer que a área do conjunto \(A\) é igual à área do rectângulo de base \([a,b]\) e altura \(f(c).\)

O integral indefinido.

Generalização do símbolo de integral.

Antes de introduzirmos o integral indefinido temos que generalizar o símbolo \[\displaystyle\int_a^b f(x)\,dx.\] Ele foi introduzido no pressuposto que \(a\lt b\). Definimos agora,

• \(\displaystyle\int_a^a f(x)\,dx=0\quad\) (reflectindo o facto da área do segmento vertical \(x=a\) entre o gráfico de \(f\) e o eixo \(0x\) ser nula)
• \(\displaystyle\int_a^b f(x)\,dx=-\int_b^a f(x)\,dx,\quad\) se \(a\gt b\).

Com estas definições pode-se ver que, independentemente da ordenação de \(a,b,c\) as propriedades 1., 2., 3. e o Teorema da Média são válidos, desde que existam os integrais da função \(f(x)\) em todos os intervalos, o que antecipamos ser verdadeiro, por exemplo, para funções contínuas. referidos.

Definição do integral indefinido.

Definição (integral indefinido).

Seja \(D\) um intervalo e \(\;f:D\to \mathbb{R},\;\) uma função integrável em qualquer intervalo limitado contido em \(D\). Fixe-se \(a\in D\). O integral indefinido de \(f\) com ponto inicial \(a\) é a função \(\;\varphi_a:D\to\mathbb{R}\;\) dada por \[\varphi_a(x)=\int_a^x f(t)\,dt.\]

Observação importante: O integral indefinido \(\int_a^xf(t)\,dt\) é uma função, o integral definido \(\int_a^bf(t)\,dt\) é um valor numérico.

Uma questão de notação: Para o integral indefinido não podemos usar para variável de integração a mesma letra que usamos para o limite de integração variável, isto é, NÃO podemos usar \(\int_a^xf(x)\,dx\) ou \(\int_a^tf(t)\,dt\). Mas é perfeitamente lícito escrevermos na forma apresentada na definição ou, por exemplo, \(\varphi_a(t)=\int_a^t f(x)\,dx\).

Veja que a propriedade de aditividade (propriedade básica 3.) implica que

• \(\displaystyle \varphi_a(x)-\varphi_b(x)=\int_a^b f(t)\,dt,\;\) é constante para todo \(\;x\in D\)
• \(\displaystyle \varphi_a(x)-\varphi_a(x_0)=\int_{x_0}^xf(t)\,dt,\;\) é independente de \(a\), para todos \(x_0, x\in D.\)

Teorema (continuidade do integral indefinido)

Seja \(D\) um intervalo e \(a\in D\). Seja \(f:D\to \mathbb{R}\) integrável em qualquer intervalo limitado contido em \(D\). Então o integral indefinido \(\varphi_a\) é uma função contínua em \(D\).

O Teorema Fundamental do Cálculo

Suponhamos que \(f\) é contínua num intervalo aberto \(D\). Fixemos \(a\in D\) e consideremos \(x,x_0\in D\). Então, pela secção anterior, \[\lim_{x\to x_0}\frac{\varphi_a(x)-\varphi_a(x_0)}{x-x_0}=\lim_{x\to x_0}\frac{1}{x-x_0}\int_{x_0}^x f(t)\,dt =\lim_{x\to x_0}f(c_x)=f(x_0)\]

Teorema Fundamental do Cálculo (TFC-1ª versão).

Se \(f\) é contínua no intervalo aberto \(D\) e \(a\in D\), então o integral indefinido \[\varphi_a(x)=\int_a^x f(t)\,dt\] é uma função diferenciável em \(D\) e, para cada \(x_0\in D\) temos, \[\varphi_a'(x_0)=f(x_0).\]

Exemplo 7. seja \(f(x)=e^{-x^2}\). Pelo TFC, podemos dizer que se \[F(x)=\int_0^x e^{-t^2}\,dt\qquad \text{então}\qquad F'(x)=e^{-x^2},\quad \forall x.\] Observa-se que, neste caso, não existe uma expressão explícita para o integral indefinido em termos das funções elementares.
Este é um exemplo de uma função que é definida por um integral indefinido: a "função erro" muito importante na estatística: \(\operatorname{erf} (x)=\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}dt.\)

Observação O Teorema Fundamental do Cálculo estabelece a ligação entre o Cálculo Diferencial (derivadas) e o Cálculo Integral (integrais). À partida nada nos fazia suspeitar que o conceito de derivada e portanto de primitiva, estivesse relacionado com o conceito de integral. Relembremos as interpretações geométricas aparentemente não relacionadas da derivada e do integral.

Teorema Fundamental do Cálculo (TFC-2ª versão): regra de Barrow

Seja \(f\) contínua em \([a,b]\) e \(F\) uma primitiva qualquer de \(f\) em \([a,b].\;\) Então, \[\int_a^b f(t)\,dt=F(b)-F(a).\]

Demonstração. O TFC diz-nos que o integral indefinido \(\;\displaystyle \varphi_a(x)=\int_a^x f(t)\,dt\;\) é uma primitiva de \(f\) em \([a,b],\) logo, para algum \(C\in\mathbb{R},\) \[F(x)=\varphi_a(x)+C\] Então, como \(\;\varphi_a(a)=0\;\) e \(\;\varphi_a(b)=\int_a^b f(t)\,dt,\;\) temos, \[\int_a^b f(t)\,dt=\varphi_a(b)=(\varphi_a(b)+C)-(\varphi_a(a)+C)=F(b)-F(a)\,.\]

Notação: escrevemos \[F(b)-F(a)=\left[F(x)\right]_a^b\,.\]

Portanto este teorema transforma o problema do cálculo de um integral num problema de primitivação. Assim, a possibilidade de encontrar uma expressão que dê o valor de um integral depende da nossa capacidade de primitivar a função a integrar.

Exemplo 8. \(\;\displaystyle \int_1^2 x^5 \,dx=\left[\frac{x^6}{6}\right]_1^2=\frac{2^6}{6}-\frac{1^6}{6}=\frac{63}{6}.\)

Exemplo 9. \(\;\displaystyle \int_0^{\pi/2} \operatorname{sen}x \,dx=\left[-\cos x\right]_0^{\pi/2}=-\cos 0+\cos\frac{\pi}{2}=1.\)

Exemplo 10. \(\;\displaystyle \int_{-\pi}^{\pi} \operatorname{sen}x \,dx=\left[-\cos x\right]_{-\pi}^{\pi}=-\cos (-\pi)+\cos\pi=1-1=0.\)

Exemplo 11. \(\;\displaystyle \int_{-\pi/2}^{\pi/2} \cos x \,dx=\left[\operatorname{sen}x\right]_{-\pi/2}^{\pi/2} =\operatorname{sen}\frac{\pi}{2}-\operatorname{sen}\left(-\frac{\pi}{2}\right)=1-(-1)=2.\)

Exemplo 12. \(\;\displaystyle \int_{1}^{2} \dfrac{1}{x} \,dx=\left[\ln |x|\right]_{1}^{2}=\ln 2-\ln 1=\ln 2.\)

Exemplo 13. \(\;\displaystyle \int_{-e^3}^{-1} \dfrac{1}{x} \,dx=\left[\ln |x|\right]_{-e^3}^{-1}=\ln 1-\ln e^3=-3.\quad\)

Exemplo 14. \(\;\displaystyle \int_{-1}^{1} \frac{1}{x^2+1} \,dx=\left[\operatorname{arctg}x\right]_{-1}^{1} =\operatorname{arctg}1-\operatorname{arctg}(-1)=\frac{\pi}{4}-\left(-\frac{\pi}{4}\right)=\frac{\pi}{2}.\)

Exemplo 15. \(\;\displaystyle \int_{0}^{1} xe^{-x^2} \,dx=\left[-\frac{e^{-x^2}}{2}\right]_{0}^{1}=\frac{1-e^{-1}}{2}.\)

Exemplo 16. \(\;\displaystyle \int_{0}^{1} \frac{x}{x^4+1} \,dx=\frac{1}{2}\int_{0}^{1} \frac{(x^2)'}{(x^2)^2+1} \,dx= \frac{1}{2}\left[\operatorname{arctg}(x^2)\right]_{0}^{1} =\frac{1}{2}(\operatorname{arctg}1-\operatorname{arctg}0)=\frac{\pi}{8}.\)

Exemplo 17. \(\;\displaystyle \int_{e}^{e^2} \dfrac{1}{x\ln x} \,dx=\int_{e}^{e^2} \dfrac{(\ln x)'}{\ln x} \,dx= \left[\ln |\ln x|\right]_{e}^{e^2}=\ln 2-\ln 1=\ln 2.\)

A regra de Barrow permite-nos transformar o problema de calcular o integral de uma função no problema de calcular uma primitiva dessa função. Desta forma podemos usar as técnicas de primitivação estudadas e, em seguida, usar a regra de Barrow. Vimos já exemplos disso em casos em que a função tinha primitiva imediata ou quase-imediata. Vemos em seguida que, em casos em que se pode calcular uma primitiva recorrendo aos métodos de primitivação por partes ou de substituição de variável, podemos usar fórmulas que contêm já esses dois passos: a fórmula de integração por partes e a fórmula de integração por substituição de variável.

Uma consequência da regra de Barrow: a fórmula de integração por partes.

Fórmula de integração por partes:

Sejam \(f,\;g\) de classe \(C^1\) em \([a,b]\). Então, \[\int_a^b f'(x)g(x)\,dx=\left[f(x)g(x)\right]_a^b-\int_a^bf(x)g'(x)\,dx\,.\]

Exemplos

1. \(\displaystyle\int_1^2x\ln x\,dx=\left[\frac{x^2}{2}\ln x\right]_{1}^{2}-\int_1^2\frac{x^2}{2}\cdot\frac{1}{x}\,dx= 2\ln 2-\left[\frac{x^2}{4}\right]_1^2 =2\ln 2 -\frac{3}{4}\,. \)
2. \(\displaystyle\int_0^1\operatorname{arctg} x\,dx=\left[x\operatorname{arctg}x\right]_{0}^{1}-\int_1^2 x\cdot\frac{1}{1+x^2}\,dx= \frac{\pi}{4}-\left[\frac{1}{2}\ln(1+x^2)\right]_0^1 =\frac{\pi}{4} -\frac{1}{2}\ln 2\,. \)
3. \(\displaystyle\int_0^\pi \cos^2x\,dx=\left[\operatorname{sen}x\cos x\right]_{0}^{\pi}-\int_0^\pi\left(-\operatorname{sen}^2x\right)\,dx= 0+\int_0^{\pi} (1-\cos^2x)\,dx=\pi-\int_0^\pi \cos^2 x\,dx\,. \)
   Somando \(\displaystyle\int_0^\pi \cos^2 x\,dx\) a ambos os membros e dividindo por \(2\), obtemos, \[\int_0^\pi \cos^2 x\,dx=\frac{\pi}{2}\,.\]
4. \(\displaystyle\int_1^\sqrt{3} \frac{1}{x^2}\operatorname{arctg}x\,dx =\left[-\frac{1}{x}\operatorname{arctg}x\right]_1^{\sqrt{3}}+\int_1^{\sqrt{3}}\left(\frac{1}{x(1+x^2)}\right)\,dx\)
   \(\displaystyle\qquad\qquad\qquad\qquad=-\frac{\pi}{3\sqrt{3}}+\frac{\pi}{4}+\int_1^{\sqrt{3}}\left(\frac{1}{x}-\frac{x}{1+x^2}\right)\,dx\)
   \(\displaystyle\qquad\qquad\qquad\qquad=-\frac{\pi}{3\sqrt{3}}+\frac{\pi}{4}+\left[\ln|x|-\frac{1}{2}\ln(1+x^2)\right]_1^{\sqrt{3}} =-\frac{\pi}{3\sqrt{3}}+\frac{\pi}{4}+\frac{1}{2}\ln\frac{3}{2}\,.\)
   Note que tivemos que usar o método de decomposição de uma função racional em fracções simples (confirme os cálculos).

Outra consequência da regra de Barrow: a fórmula de integração por substituição de variável

Já sabemos que, por vezes, é útil substituir uma primitivação por uma outra para a qual temos um método de resolução através de uma substituição de variável. O mesmo se passa com a integração:

Fórmula de integração por substituição de variável.

Sejam \(I,J\) intervalos, \(f:J\to\mathbb{R}\) contínua, \(u\) de classe \(C^1\) e injectiva em \(I\) com \(J=u(I).\) Então, dados \(a,b\in J\), \[ \int_a^b f(x)\,dx=\int_{u^{-1}(a)}^{u^{-1}(b)}f\left(u(t)\right)u'(t)\,dt\,. \]

Demonstração

Tal como já referido relativamente à primitivação, aqui também é conveniente usar a notação \[\frac{dx}{dt}=u'(t),\]

Portanto, para integrar por substituição fazendo \(x=u(t)\):

1. substitui-se na função a integrar \(x\) por \(u(t)\);
2. multiplica-se a função a integrar por \(\frac{dx}{dt}\)
3. faz-se \(\begin{cases}x=a &\Rightarrow t=u^{-1}(a)\\x=b &\Rightarrow t=u^{-1}(b)\end{cases};\)
4. Calcula-se a primitiva na variável \(t\) e usa-se a regra de Barrow entre \(u^{-1}(a)\) e \(u^{-1}(a)\).

Reparem que, ao usar este procedimento não temos que calcular explicitamente a primitiva de \(f(x)\) contrariamente ao que tínhamos feito na primitivação (ver guia de estudo da aula teórica 28): não precisamos agora de calcular a inversa \(t=u^{-1}(x)\), em vez disso, temos que ver qual o intervalo em \(t\) no qual o intervalo em \(x\), \([a,b]\), se transforma.

Exemplos

1. Calcular \(\displaystyle \int_1^2\frac{e^{\sqrt{x}}}{\sqrt{x}}\,dx\;.\qquad\) A forma da função sugere que se faça \(\;t=\sqrt{x}.\)
   Então \(x=t^2\) e, portanto, \(\dfrac{dx}{dt}=2t\,.\)
   Além disso, \(\begin{cases}x=1 &\Rightarrow t=1\\x=2 &\Rightarrow t=\sqrt{2}.\end{cases}\) Logo, a fórmula de substituição escreve-se, \[\int_1^2\frac{e^{\sqrt{x}}}{\sqrt{x}}\,dx= \int_1^{\sqrt{2}}\frac{e^{t}}{t}\cdot\frac{dx}{dt}\,dt =\int_1^{\sqrt{2}}\frac{e^{t}}{t}\cdot2t\,dt=\left[2e^t\right]_ 1^{\sqrt{2}}=2e^{\sqrt{2}}-2e.\] Reparem que a primitiva também se poderia resolver como quase-imediata. Isto é geral: qualquer primitiva quase-imediata pode ser convertida numa imediata através de uma substituição de variável.
2. Calcular \(\displaystyle\int_{1/e}^1\frac{\ln x}{x(\ln x-1)^2}\,dx.\qquad\) Faz-se \(t=\ln x.\)
   Então \(x=e^t\) e, portanto, \(\dfrac{dx}{dt}=e^t\,.\)
   Além disso, \(\begin{cases}x=1/e &\Rightarrow t=-1\\x=1 &\Rightarrow t=0.\end{cases}\qquad\) Logo, a fórmula de substituição escreve-se, \[\begin{aligned}\int_{1/e}^1\frac{\ln x}{x(\ln x-1)^2}\,dx&=\int_{-1}^0 \frac{t}{e^t(t-1)^2}\frac{dx}{dt}\,dt= \int_{-1}^0 \frac{t}{e^t(t-1)^2}e^t\,dt= \int_{-1}^0 \frac{t}{(t-1)^2}\,dt\\ &=\int_{-1}^0 \frac{t-1+1}{(t-1)^2}\,dt=\int_{-1}^0 \left(\frac{1}{t-1}+\frac{1}{(t-1)^2}\right)\,dt\\&= \left[\ln |t-1|-\frac{1}{t-1}\right]_{-1}^0=1-\ln 2-\frac{1}{2}=-\ln 2-\frac{1}{2}.\end{aligned}\]
3. Calcular \(\displaystyle\int_{1/2}^1\frac{1}{x^3}e^{1/x}\,dx.\qquad\) Faz-se \(t=1/x.\)
   Então, \(\;x=1/t\;\) e \(\;\dfrac{dx}{dt}=-\dfrac{1}{t^2}\)
   Além disso, \(\begin{cases}x=1/2 &\Rightarrow t=2\\x=1 &\Rightarrow t=1.\end{cases}\qquad\) Logo, a fórmula de substituição escreve-se, \[\begin{aligned}\int_{1/2}^1\frac{1}{x^3}e^{1/x}\,dx&=\int_{2}^1 t^3e^{t}\frac{dx}{dt}\,dt =\int_{2}^1 t^3e^{t}\left(-\dfrac{1}{t^2}\right)\,dt\\&=\int_1^{2} te^{t}\,dt=[te^t]_{1}^2-\int_1^2e^t\,dt=2e^2-e-[e^t]_1^2=e^2.\end{aligned}\]
4. Calcular \(\displaystyle\int_{0}^{\pi/4}\frac{1-\operatorname{tg}x}{1+\operatorname{tg}x}\,dx.\qquad\) Faz-se \(t=\operatorname{tg}x.\)
   Então, \(\;x=\operatorname{arctg}t\;\) e \(\;\dfrac{dx}{dt}=\dfrac{1}{1+t^2}.\)
   Além disso, \(\begin{cases}x=0 &\Rightarrow t=0\\x=\pi/4 &\Rightarrow t=1.\end{cases}\qquad\) Logo, a fórmula de substituição escreve-se, \[\int_{0}^{\pi/4}\frac{1-\operatorname{tg}x}{1+\operatorname{tg}x}\,dx=\int_0^1\frac{1-t}{(1+t)(1+t^2)}dt =\left[\ln|t+1|-\frac{1}{2}\ln(1+t^2)\right]_0^1=\frac{1}{2}\ln 2.\] Faça os detalhes da integração da função racional.
5. Calcular \(\displaystyle\int_{1}^4\frac{1}{\sqrt{x}}\ln(x+\sqrt{x})\,dx.\qquad\) Faz-se \(t=\sqrt{x}.\)
   Então \(\;x=t^2\;\) e \(\;\dfrac{dx}{dt}=2t\;\) Além disso, \(\begin{cases}x=1 &\Rightarrow t=1\\x=4 &\Rightarrow t=2.\end{cases}\qquad\) Logo, a fórmula de substituição escreve-se, \[\begin{aligned}\int_{1}^4\frac{1}{\sqrt{x}}\ln(x+\sqrt{x})\,dx&=\int_1^2 \frac{1}{t}\ln(t^2+t)2t\,dt=\int_1^2 2\ln(t^2+t)\,dt\\ &=[2t\ln(t^2+t)]_1^2-\int_1^2 2t\frac{2t+1}{t^2+t}\,dt=4\ln 6-2\ln 2-2\int_1^2\frac{2t+1}{t+1}\,dt\\ &=2\ln 18-2\int_1^2\left(2-\frac{1}{t+1}\right)dt=2\ln 18-4+2\ln 5-2\ln 3=2\ln 30-4.\end{aligned}\] Veja que aqui se usou a fórmula de integração por partes depois de se ter usado a de substituição de variável. Faça os detalhes da integração da função racional.

Observação. Como vimos nos exemplos, as substituições são em geral sugeridas pela função integranda. Quando isso não acontece, (como provavelmente do exemplo 5) a substituição será dada no exercício. É o que acontece com as seguintes substituições apesar de elas serem standard:

Substituições standard para integração de raizes (serão dadas):

• \(\sqrt{a^2-x^2},\;\) com \(\;x^2\leqslant a^2:\quad\) faz-se \(\;x=a\operatorname{sen}t\;\) ou \(\;x=a\cos t.\)
• \(\sqrt{a^2-x^2},\;\) com \(\;x^2\geqslant a^2:\quad\) faz-se \(\;x=a\dfrac{1}{\cos^2 t}\;\) ou \(\;x=a\cosh t.\)
• \(\sqrt{a^2+x^2}:\quad\) faz-se \(\;x=a\operatorname{tg}x\;\) ou \(\;x=a\operatorname{senh} t.\)

Exemplo 6. Calcular \(\displaystyle\int_{1/2}^{\sqrt{2}/2}\frac{\sqrt{1-x^2}}{x^2}\,dx\,.\quad\) Faz-se \(x=\cos t\).
Então \(\dfrac{dx}{dt}=-\operatorname{sen} t,\;\) e \(\;\begin{cases}x=1/2 &\Rightarrow t=\pi/3\\x=\sqrt{2}/2 &\Rightarrow t=\pi/4.\end{cases}\qquad\) Logo, \[\int_{1/2}^{\sqrt{2}/2}\frac{\sqrt{1-x^2}}{x^2}\,dx=\int_{\pi/3}^{\pi/4}\frac{\sqrt{1-\cos^2 t}}{\cos^2 t}(-\operatorname{sen}t)\,dt =\int_{\pi/4}^{\pi/3}\operatorname{tg}^2t\,dt=\int_{\pi/4}^{\pi/3}((1+\operatorname{tg}^2t)-1)\,dt\] \[=[\operatorname{tg}t-t]_{\pi/4}^{\pi/3}= \sqrt{3}-1-\frac{\pi}{12}.\]

Exercício: Usando a substituição \(t=-x\) mostre que: \[\int_{-a}^0 f(x)\,dx=\int_0^a f(-t)\,dt.\] Daqui tira-se:

• Se \(f\) é par (\(f(-x)=f(x)):\qquad\) \(\displaystyle\int_{-a}^a f(x)\,dx=2\int_0^af(x)\,dx\)
• Se \(f\) é ímpar (\(f(-x)=-f(x)):\qquad\) \(\displaystyle\int_{-a}^a f(x)\,dx=0\)