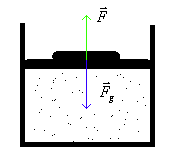
(
- 2.a)
- Determine a solução particular da equação para as oscilações do corpo que corresponde a oscilações com amplitude constante. Qual o valor da amplitude e da diferença de fase entre as oscilações e a força exterior.
- 2.b)
- Se pretendesse aumentar
a resposta do sistema variando a frequência
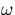 como procederia?
Qual o valor máximo da amplitude das ascilações
do corpo considerando que a amplitude da força exterior
tem um valor máximo de 3 N?
como procederia?
Qual o valor máximo da amplitude das ascilações
do corpo considerando que a amplitude da força exterior
tem um valor máximo de 3 N?