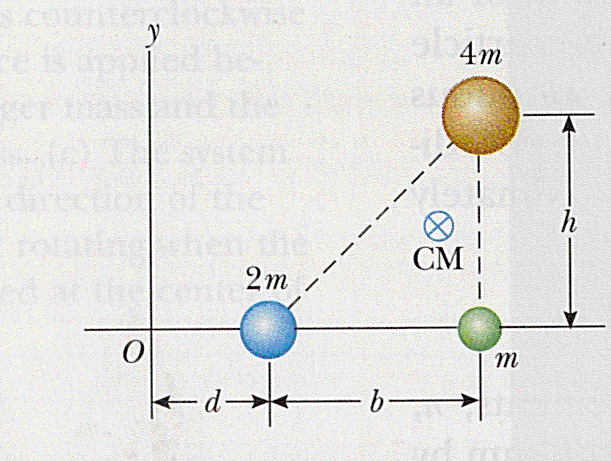
Determine as coordenadas do centro de massa do sistema.
Física I para LEIC
1999/2000
Semana de 17/04/2000 a 18/04/2000 & de 26/04/2000 a 28/04/2000

Determine as coordenadas do centro de massa do sistema.
![]()
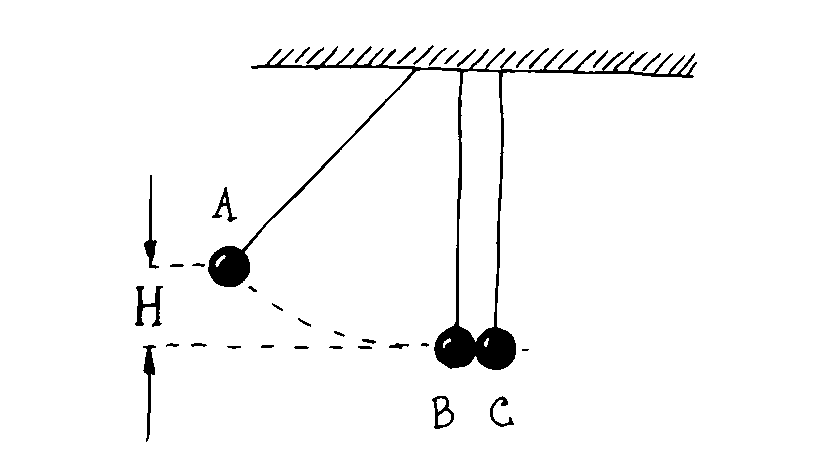
No instante inicial, A é largado da altura h com velocidade inicial nula.
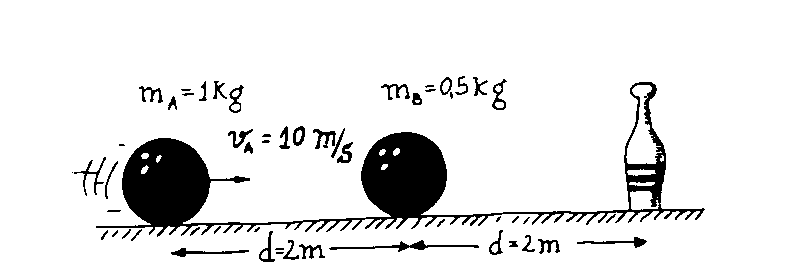
![]()
onde ![]() é a massa reduzida do sistema.
é a massa reduzida do sistema.
![]()
![]()
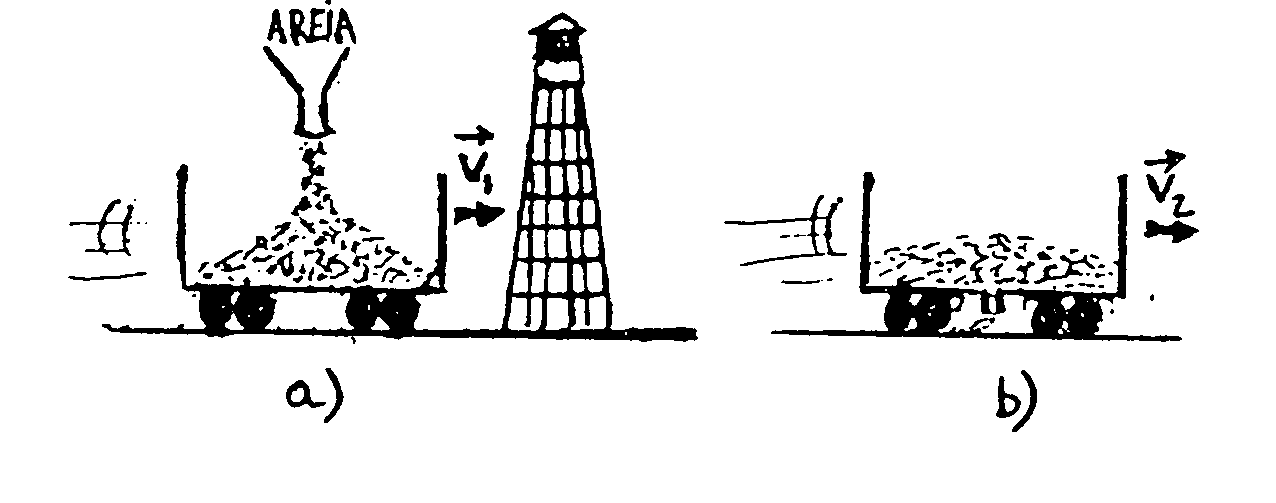
Nesse instante começa a receber areia de uma tremonha fixa ao solo. A massa total de areia recebida é de 200 kg.