3^a Série de problemas

Física I para LEIC

1999/2000

Semana de 27/03/2000 a 31/03/2000

1.

([Ser] Exemplo 6.1, pag. 146) Uma bola é posta a girar presa a uma corda de comprimento r = 1.50 m. Sabendo que a massa da bola é m=0.5 kg e que a corda pode suportar tensões até 50 N, determine:

1.a)

a velocidade máxima que poderá atingir a bola sem que a corda parta.

1.b)

a tensão na corda quando a velocidade da bola é 5 m/s.

2.

( [Ser] Exemplo 6.2, pag. 146- Pêndulo cónico.)
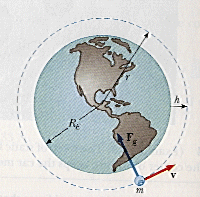
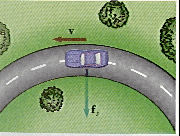
Um pequeno corpo de massa m suspenso numa corda de comprimento L descreve um cículo de raio r com uma velocidade v. Durante este movimento a corda descreve uma superfície cónica e faz um angulo $\theta$com a vertical.

2.a)

Calcule a velocidade do corpo v em função de $\theta$.

2.b)

Calcule período de revolução T, correspondente ao intervalo de tempo necessário para que o corpo dê uma volta completa.

3.

([Ser] Exemplo 6.5, pag. 148 - Movimento de um satélite.) Neste exercício pretende-se analisar o movimento de um satélite que descreve uma órbita circular em torno da Terra. Para entender este movimento é necessário recordar que a força gravítica que actua entre duas massas m₁ e m₂ a uma distância relativa r é dada pela lei de Newton sendo o seu módulo dado por:

$$F=G\frac{m_1 m_2}{r^2}$$ (1)

onde $G=6.67\times 10^{-11}$N m²/kg² é a constante de gravitação universal.

Considere um satélite que se move com uma velocidade v em órbita circular em torno da Terra e a uma altitude h sobre a superfície.

3.a)

Calcule a velocidade do corpo em função de $h, \, R_{\oplus},$ e G, onde $R_{\oplus}$ é o raio médio da Terra.

3.b)

Calcule período do satétile se a órbita estiver a uma altitude h=350 km. Considere $R_{\oplus}$ = 6400 km.

4.

([Ser] Exemplo 6.10, pag. 156 - Queda de um corpo num meio com atrito)
Uma pequena esfera de massa m=2g é deixada cair num tubo com óleo sendo a sua velocidade limite de v=5 cm/s.

4.a)

Represente as forças que actuam na esfera e escreva a equação do movimento da esfera.

4.b)

Ao fim de quanto tempo a esfera atinge $90 \%$ da velocidade limite?

5.

([Ser] Exemplo 6.3, pag. 147])
Um carro de massa m= 1500 kg descreve uma curva de raio r=35m, como se pode ver na figura. Se o coeficiente de atrito estático entre os pneus e o piso seco fôr 0.5, calcule a velocidade máxima que o carro pode ter para conseguir fazer a curva, sem se despistar.

6.

Um automóvel deslocando-se a 48 km/h pode travar completamente em 40 m. Se esse automovel seguir a 96 km/h qual é a distância mínima de travagem?

7.

Considere uma mulher de massa 50 kg no interior do elevador. Calcule o seu peso quando

7.a)

O elevador inicia a subida com uma aceleração$\ a_0=1ms^{-2}$.

7.b)

O elevador inicia a descida com uma aceleração$\ a_0=1.5 ms^{-2}$.

8.

8.a)

Um rio corre para sul com velocidade v na latitude de 45^oN. Qual a força de Coriolis que actua numa massa m de água? Qual das suas margens sofre maior erosão?

8.b)

Considere um ponto à superfície da Terra. A direcção de um fio de prumo e a direcção radial (em geral) não coincidem. Porquê? Em que pontos da superfície da Terra estas direcçõescoincidem?

3/28/2000