Programa
 
 

Capítulo 1

Grupos Topológicos e Grupos de Lie.

-

Grupos topológicos e grupos de Lie. Grupo das componentes e exemplos.

-

Teorema da geração finita de um grupo topológico conexo. Homotopia de aplicações e grupo fundamental de um espaço topológico. Carácter abeliano do grupo fundamental de um grupo topológico conexo.

-

Revestimento universal de grupos topológicos conexos e exemplos.

-

Campos vectoriais e 1-formas diferenciais invariantes à esquerda (e direita) num grupo de Lie. Subgrupos a um parâmetro de grupos de Lie e álgebra de Lie, Lie(H), de um grupo de Lie, G. Subgrupos e subalgebras.

-

Grupos localmente isomorfos. Homomorfismos e teorema de Lie. Exemplos. Aplicação exponencial.

-

Acções de um grupo de Lie em variedades diferenciais. Representações em espaços lineares. Representações de Lie(H) correspondentes a representações de G.

 

Neste capítulo introdutório são discutidos resultados gerais de grupos topológicos [5] e introduzidos grupos de Lie [1, 3, 6, 7].
É recordado o conceito de variedade e são introduzidos grupos de Lie e estudadas algumas das suas propriedades. O objectivo desta parte consiste em recordar alguns conceitos. As referências mais usadas são [1, 3, 6, 7].
 
  Capítulo 2

Álgebras de Lie

-

Álgebras de Lie reais e complexas. Somas directas e semi-directas de álgebras de Lie.

-

Ideais, solvabilidade e nilpotência. Critérios de Cartan. Decomposição de Levi.

 

No curso estudam-se com maior profundidade álgebras e grupos de Lie semi-simples. No entanto são estudados no presente capítulo alguns resultados gerais.
 
  Capítulo 3

Álgebras de Lie complexas semi-simples

-

Subalgebras de Cartan e raízes. Representações de 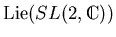${\rm Lie}(SL(2,{\mathchoice{\setbox0=\hbox{$\displaystyle\rm C$}\hbox{\hbox to......tstyle\rm C$}\hbox{\hbox to0pt{\kern0.4\wd0\vrule height0.9\ht0\hss}\box0}}}))$. Álgebras$A_l = {\rm Lie}(SL(l+1,{\mathchoice{\setbox0=\hbox{$\displaystyle\rm C$}\hbox{......tstyle\rm C$}\hbox{\hbox to0pt{\kern0.4\wd0\vrule height0.9\ht0\hss}\box0}}}))$.

-

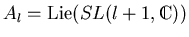Matriz de Cartan e diagramas de Dynkin. Grupo de Weyl. Álgebras clássicas. Classificação das álgebras de Lie simples.

-

Construção da álgebra semi-simples correspondente a uma matriz de Cartan.

 

Este capítulo é uma parte muito importante do curso uma vez que contém não só a classificação das algebras de Lie complexas simples mas também porque os resultados aqui obtidos são centrais para os dois capítulos seguintes. As referências mais usadas são [1,2] mas também [8,9].
 
  Capítulo 4

Representações de Álgebras de Lie complexas semi-simples

-

Pesos e correspondente decomposição do espaço da representação em espaços próprios da subalgebra de Cartan.

-

Produtos tensoriais de representações e diagramas de Young.

-

Decomposição de representações de álgebras em representações de subalgebras.

-

Aplicações em modelos de física de partículas elementares.

 

No capítulo 4 ilustram-se os resultados obtidos nos primeiros 3 parágrafos com aplicações a modelos de física de partículas ditos de unificação das interacções. As referências seguidas são [1, 2, 10, 11].
 
  Capítulo 5

Formas Reais

-

Formas reais de álgebras de Lie. Formas reais compactas. Teorema de Weyl.

-

Decomposição de Cartan.

-

Representações unitárias de grupos de Lie compactos.

 

Neste capítulo estudam-se formas reais compactas e não compactas de álgebras de Lie. Estudam-se representações unitárias irredutíveis de grupos compactos [1, 2, 7, 11].
 
  Capítulo 6

Espaços homogéneos

-

Campos tensoriais invariantes e bi-invariantes (i.e. invariantes no espaço homogéneo  GxG/diag(G)) num grupo de Lie G.

-

Existência e classificação de campos tensoriais invariantes em espaços homogéneos redutivos. Espaços simétricos.

-

Métricas pseudo-riemannianas invariantes e aplicações às equações de Einstein.

 

No capítulo 6 estudam-se diferentes aspectos da geometria invariante em espaços homegéneos G/H de grupos de Lie. Particular ênfase é dada à redução do problema de encontrar campos tensorias invariante pela acção de G e ao problema algébrico de determinar tensores invariantes em relação à acção do grupo de isotropia no espaço tangente a um ponto. A referência mais usada é [4, Cap. X, XI]. Como ilustração refere-se a redução das equações de Einstein, no caso de métricas invariantes em espaços homogéneos, a equações algébricas.
 
 

Observações

O programa foi elaborado para um semestre com 13 semanas efectivas, com 3h de aulas por semana.

A distribuição prevista das semanas por capítulo será, aproximadamente, a seguinte:
 

Cap. 1- Grupos Topológicos e Grupos de Lie 4
Cap. 2- Álgebras de Lie 1
Cap. 3- Álgebras de Lie complexas semi-simples 3
Cap. 4- Representações de álgebras de Lie complexas semi-simples 2
Cap. 5- Formas Reais 1
Cap. 6- Espaços homogéneos 2
 

Na escolha do programa tiveram particular influência os livros de Varadarajan [1], Goto e Grosshans [2], e Kobayashi, Nomizu [3,4].