Pode ser visto como o resultado de fazer rodar, em torno do eixo \(Oz\), a circunferência de raio igual a 1 e centro no ponto \((0,4,0)\), representada na figura seguinte:

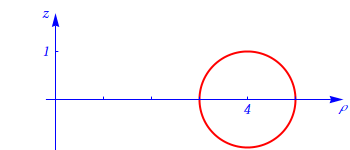
Note-se que \(\rho=\sqrt{x^2+y^2}\) é a distância do ponto de coordenadas \((x,y,z)\) ao eixo \(Oz\). Portanto, \[(\rho-4)^2+z^2=1\] e, fazendo rodar esta circunferência, em torno do eixo \(Oz\), obtém-se o toro de raios 4 e 1.

Pode também ser visto como uma "pilha" ou colecção de duas circunferências na direcção \(Oz\). De facto, da equação de definição, obtém-se \[\sqrt{x^2+y^2}=4 \pm \sqrt{1-z^2},\] e, portanto, para cada \(z\) fixo entre \(-1\) e \(1\), há duas circunferências de raios \(4 - \sqrt{1-z^2}\) e \(4 + \sqrt{1-z^2}\), respectivamente.

Conjunto de nível zero da função \(F:\mathbb{R}^3 \to \mathbb{R}\), definida por \(F(x,y,z)= \left(\sqrt{x^2+y^2}-4\right)^2 + z^2 -1\).