Gráfico da função escalar \(f:\mathbb{R}^2 \to \mathbb{R}\), definida por, \(f(x,y)=(y-x^2)(y-3x^2)\).

A origem \((0,0)\) é o único ponto de estacionaridade da função \(f\) mas não é extremo. De facto, tem-se \begin{cases} \frac{\partial f}{\partial x}=-8xy+12x^3=0 \\ \frac{\partial f}{\partial y}=2y-4x^2=0, \end{cases} de onde se conclui que a origem é o único ponto de estacionaridade.

A matriz hesseana é dada por \begin{bmatrix} -8y+36x^2 & -8x \\ -8x & 2 \end{bmatrix} e na origem será \begin{bmatrix} 0 & 0 \\ 0 & 2 \end{bmatrix} e, portanto, um dos valores próprios é nulo. Sendo \(f(0,0)=0\) é conveniente fazer a análise local do sinal da função \(f\) em torno da origem.

Note-se que, sendo \(f\) um produto, se tem \(f(x,y) \geq 0\) para \(y \geq 3x^2\) bem como para \(y\leq x^2\).

Por outro lado, \(f(x,y)\leq 0\) para \(x^2\leq y \leq 3x^2\), tal como se mostra na figura seguinte:

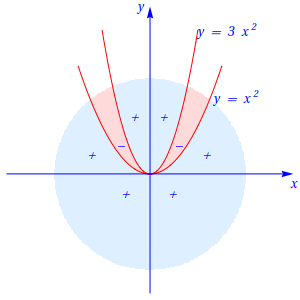
Assim, a origem não é ponto de extremo de \(f\).

Note-se que a análise local do sinal de \(f\) em torno da origem é essencial porque o teste de segunda ordem não permite a classificação do ponto de estacionaridade.

De facto, dado que um dos valores próprios da matriz hesseana é 2, a origem apresenta-se como ponto de mínimo na respectiva direcção própria. Por outro lado, a direcção própria associada ao valor próprio \(\lambda =0\) é dada pelo vector \((1,0)\). Assim, nesta direcção, tem-se \(f(x,0)=3x^4\) e, portanto, a origem apresenta-se como ponto de mínimo de \(f\). A análise local contraria estas conclusões. Portanto, o teste de segunda ordem não permite a classificação do ponto de estacionaridade.