Colecção ou "pilha" de circunferências de raio \(\sqrt{z}\) e centro em \((0,0,z)\). De facto, em cada plano \(z=z_0\), com \(0 \leq z_0 \leq 1\), encontra-se a circunferência dada pela equação \(x^2+y^2=z_0\).

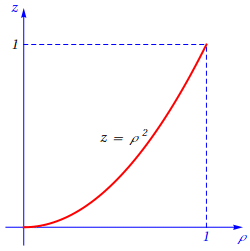
Fazendo \(\rho=\sqrt{x^2+y^2}\), que designa a distância do ponto de coordenadas \((x,y,z)\) ao eixo \(Oz\), o parabolóide pode ser visto como o resultado de fazer rodar, em torno do eixo \(Oz\), o ramo de parábola definido pela equação, \(z=\rho^2\), e representado na figura seguinte:

Conjunto de nível zero da função \(F:\mathbb{R}^3 \to \mathbb{R}\), definida por \(F(x,y,z)=z-x^2-y^2\), em que \(0 \leq z \leq 1\).

Gráfico da função \(f(x,y)=x^2+y^2\), em que \(x^2+y^2 \leq 1\).

A origem \((0,0)\) é o mínimo absoluto da função \(f\). De facto, \(f(x,y) \geq 0\) e \(f(x,y)=0 \iff (x,y)=(0,0)\).