Gráfico da função escalar \(f(x,y)=\sqrt{x^2+y^2}\), sendo \(x^2+y^2 \leq 1\).

Colecção ou "pilha" de circunferências de raio igual a \(z\) e centro em \((0,0,z)\). De facto, em cada plano \(z=z_0\), com \(0 \leq z_0 \leq 1\), encontra-se a circunferência dada pela equação \(x^2+y^2=z_0^2\).

Fazendo \(\rho=\sqrt{x^2+y^2}\), que designa a distância do ponto de coordenadas \((x,y,z)\) ao eixo \(Oz\), o cone pode ser visto como o resultado de fazer rodar, em torno do eixo \(Oz\), o segmento de recta definido pela equação, \(z=\rho\), e representado na figura seguinte:

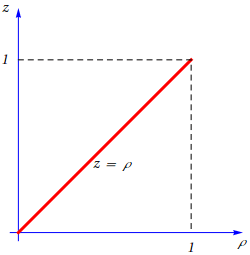
Conjunto de nível zero da função \(F:\mathbb{R}^3 \to \mathbb{R}\), definida por \(F(x,y,z)=z^2-x^2-y^2\), em que \(0 \leq z \leq 1\).

---

A função \(f: \mathbb{R}^2 \to \mathbb{R}\) definida por \(f(x,y)=\sqrt{x^2+y^2}\) é contínua na origem porque \(|f(x,y)| = ||(x,y)||.\)

Dado que \(f(x,0)=|x|,\) a derivada parcial \(\displaystyle{\frac{\partial f}{\partial x}(0,0) = \lim_{x \to 0} \frac{|x|}{x}}\) não existe e, portanto, a função \(f\) não é diferenciável na origem.