\(0 \lt z \lt x^2-y^2 \;;\; x^2+y^2 \lt 1 \;;\; x \gt 0\)

Cortes perpendiculares ao eixo \(Ox\)
Da definição é claro que se tem \(0 \lt x \lt 1\).
É também claro que \(y^2 \lt 1-x^2\) e \(y^2 \lt x^2-z \lt x^2\), ou seja, há dois casos a considerar.
Se \(x^2 \lt 1-x^2 \Leftrightarrow 2x^2 \lt 1 \Leftrightarrow x^2 \lt \frac 1 2,\) então, fixando a coordenada \(x\) entre \(0\) e \(\frac{\sqrt{2}}{2}\), obtém-se: \[-x \lt y \lt x \,;\, 0 \lt z \lt x^2-y^2 ,\] tal como se mostra na figura seguinte:
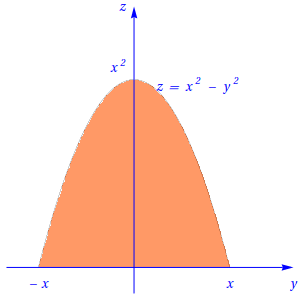
Se \(x^2 \gt 1-x^2 \Leftrightarrow 2x^2 \gt 1 \Leftrightarrow x^2 \gt \frac 1 2,\) então, fixando a coordenada \(x\) entre \(\frac{\sqrt{2}}{2}\) e \(1\), obtém-se: \[-\sqrt{1-x^2} \lt y \lt \sqrt{1-x^2} \,;\, 0 \lt z \lt x^2 -y^2,\] tal como se mostra na figura seguinte:
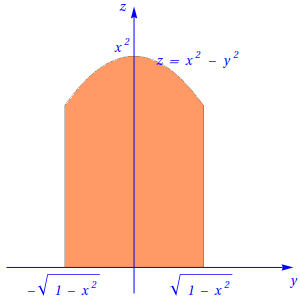
Cortes perpendiculares ao eixo \(Oy\)
Da definição, tem-se \(y^2 \lt x^2\lt 1- y^2,\) de onde se conclui que \(y^2 \lt 1- y^2 \Leftrightarrow 2y^2 \lt 1,\) ou seja, \[-\frac{\sqrt{2}}{2} \lt y \lt \frac{\sqrt{2}}{2}.\] Portanto, o corte perpendicular ao eixo \(Oy\) fica definido por \[|y| \lt x \lt \sqrt{1-y^2} \,;\, 0 \lt z \lt x^2-y^2,\] tal como se mostra na figura seguinte:
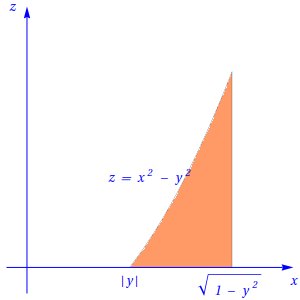
Cortes perpendiculares ao eixo \(Oz\)
Da definição, deduz-se que \(0 \lt z \lt x^2-y^2 \lt x^2 \lt 1.\)
Por outro lado, tem-se \(y^2 \lt x^2-z \lt 1-y^2 -z\), ou seja, \(2y^2 \lt 1-z \Leftrightarrow -\sqrt{\frac{1-z}{2}} \lt y \lt \sqrt{\frac{1-z}{2}}.\)
Assim, fixando \(z\) entre 0 e 1, o correspondente corte é limitado por um arco de círcunferência e por um ramo de hipérbole, ou seja, \[0 \lt z \lt 1 \,;\, -\sqrt{\frac{1-z}{2}} \lt y \lt \sqrt{\frac{1-z}{2}} \,;\, \sqrt{z+y^2} \lt x \lt \sqrt{1-y^2},\] tal como se mostra na figura seguinte:
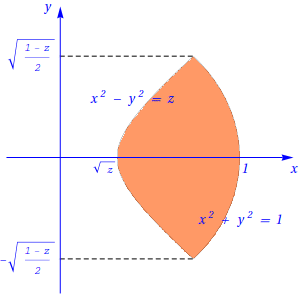
Cálculo do volume
Seja \(X\) o sólido. Em coordenadas colíndricas \((\rho, \theta, z)\) tem-se \(0 \lt \rho \lt 1\) porque \(x^2+y^2 \lt 1.\)
Dado que \(x\gt 0\) e \(y^2 \lt x^2\), então \(-\frac \pi 4 \lt \theta \lt \frac \pi 4\).
Sendo \(0 \lt z \lt x^2-y^2\), então \(0\lt z \lt \rho^2(\cos^2\theta - \sen^2\theta)=\rho^2\cos(2\theta)\).
Assim, tem-se \[\begin{align}\vol_3(X) &=\int_0^1 \left(\int_{-\pi/4}^{\pi/4}\left(\int_0^{\rho^2\cos(2\theta)}\rho dz\right)d\theta\right)d\rho \\ &= \int_0^1 \left(\int_{-\pi/4}^{\pi/4} \rho^3 \cos(2\theta)d\theta\right)d\rho \\ &=\frac 1 4.\end{align}\]