\(\frac{x^2}{4}+\frac{y^2}{4}+\frac{z^2}{9}\lt 1\)

Cortes perpendiculares ao eixo \(Ox\)

Da definição, conclui-se facilmente que \(-2 \lt x \lt 2\). Fixando \(x\) nesse intervalo, obtém-se \[\frac{y^2}{4} + \frac{z^2}{9} \lt 1 - \frac{x^2}{4}.\] Portanto, os cortes perpendiculares ao eixo \(Ox\) são elipses e encontram-se representadas na figura seguinte:

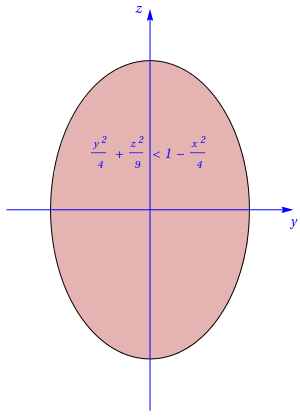
Cortes perpendiculares ao eixo \(Oz\)

Da definição, também se conclui facilmente que \(-3 \lt z \lt 3\). Fixando \(z\) nesse intervalo, obtém-se \[\frac{x^2}{4} + \frac{y^2}{4} \lt 1 - \frac{z^2}{9} , \] ou seja, \[ x^2 + y^2 \lt 4 (1 - \frac{z^2}{9}).\] Portanto, os cortes perpendiculares ao eixo \(Oz\) são círculos centrados na origem e de raio \(\frac{2}{3} \sqrt{9-z^2}.\) Encontram-se representados na figura seguinte:

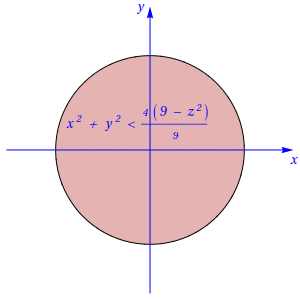
Cálculo do volume

Seja \(X\) o elipsóide e considerem-se os cortes \(C(z)\), perpendiculares ao eixo \(Oz\): \[C(z)=\{(x,y): \, x^2 + y^2 \lt \frac 4 9 (9-z^2)\}, \quad -3 \lt z \lt 3.\] Pelo Teorema de Fubini, tem-se \[\vol_3(X)=\int_{-3}^{3} \vol_2(C(z))dz.\] Dado que o corte \(C(z)\) é um círculo, tal como se mostra na Fig. 2, então \[\vol_2(C(z))=\pi \frac 4 9 (9-z^2) \] e, portanto, \[\begin{align} \vol_3(X) &=\frac {4\pi} 9 \int_{-3}^{3} (9-z^2)dz \\ & =\frac {8\pi} 9 \int_{0}^{3} (9-z^2)dz \\ & =16\pi.\end{align} \]