\( x^2+y^2 \lt 1\;;\; x^2+z^2 \lt 1\)

Cortes perpendiculares ao eixo \(Ox\)

Da definição do sólido é claro que $x^2<1$, ou seja, $-1<x<1$.

Portanto, fixando a variável x no intervalo, $-1<x<1$, obtêm-se as inequações de definição do corte perpendicular ao eixo \(Ox\): \(y^2 \lt 1-x^2 \;;\; z^2 \lt 1-x^2,\) ou seja, \[-\sqrt{1-x^2} \lt y \lt \sqrt{1-x^2} \;;\; -\sqrt{1-x^2} \lt z \lt \sqrt{1-x^2}.\] Assim, os cortes perpendiculares ao eixo \(Ox\) são quadrados tal como se representam na figura seguinte:

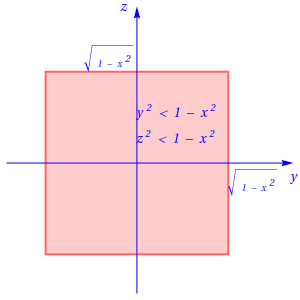
Cortes perpendiculares ao eixo \(Oy\)

Da definição do sólido é claro que $y^2<1$, ou seja, $-1<y<1$.

Portanto, fixando a variável y no intervalo, $-1<y<1$, obtém-se: \[x^2 \lt 1-y^2 \;;\; x^2+z^2 \lt 1.\]

Assim, os cortes perpendiculares ao eixo \(Oy\) têm a forma que se representa na figura seguinte:

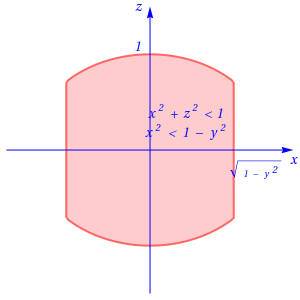
Cortes perpendiculares ao eixo \(Oz\)

Da definição do sólido é claro que $z^2<1$, ou seja, $-1<z<1$.

Portanto, fixando a variável \(z\) no intervalo, $-1<z<1$, obtém-se: \[x^2 \lt 1-z^2 \;;\; x^2+y^2 \lt 1,\] cuja forma se apresenta na figura seguinte:

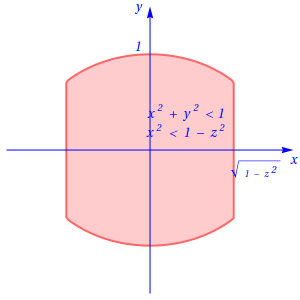
Cálculo do volume

Seja \(X\) o sólido e considerem-se os cortes \(C(x)\), perpendiculares ao eixo \(Ox\): \[C(x)=\left\{(y,z): \, |y| \lt \sqrt{1-x^2}\;;\; |z| \lt \sqrt{1-x^2} \right\}, \quad -1 \lt x \lt 1.\] Pelo Teorema de Fubini, tem-se \[\vol_3(X)=\int_{-1}^{1} \vol_2(C(x))dx.\] Dado que o corte \(C(x)\) é um quadrado, tal como se mostra na Fig. 1, então \[\vol_2(C(x))= 4\left(\sqrt{1-x^2}\right)^2=4 \left(1-x^2\right)\] e, portanto, \[\begin{align} \vol_3(X) & =4\int_{-1}^{1} \left(1-x^2\right)dx \\ & = 8\int_{0}^{1} \left(1-x^2\right)dx \\ & =\frac{16}{3}.\end{align} \]