\(\frac{1}{4} \lt x^2+y^2 \lt 1 \;;\;z^2 \lt x^2+y^2 \;;\; z \gt 0\)

Cortes perpendiculares ao eixo \(Ox\)

Da definição é claro que $-1<x<1$. Sabendo que $\frac{1}{4}<x^2+y^2<1$, há dois casos a considerar: um para $|x|<\frac{1}{2}$ e outro para $\frac{1}{2}<|x|<1$.

Assim, para o caso em que $\frac{1}{2}<|x|<1$, tem-se $y^2<1-x^2$, e o corte correspondente é o conjunto definido por \[ \cases{ -\sqrt{1-x^2} \lt y \lt \sqrt{1-x^2} \cr\cr 0 \lt z \lt \sqrt{x^2+y^2}, } \] tal como se mostra na figura seguinte:

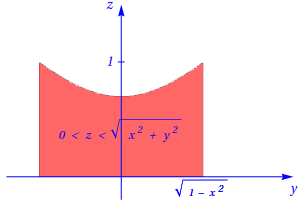
Para o caso em que $|x|<\frac{1}{2}$, tem-se $\frac{1}{4}-x^2<y^2<1-x^2$, e o corte correspondente é a união de dois conjuntos.

Para $y<0$, o corte é dado por \[ \cases{ -\sqrt{1-x^2} \lt y \lt -\sqrt{\frac{1}{4}-x^2} \cr\cr 0 \lt z \lt \sqrt{x^2+y^2}. } \] Para $y>0$, o corte é definido por \[ \cases{ \sqrt{\frac{1}{4}-x^2} \lt y \lt \sqrt{1-x^2} \cr\cr 0 \lt z \lt \sqrt{x^2+y^2}, } \] tal como se mostra na figura seguinte:

Cortes perpendiculares ao eixo \(Oz\)

O cilindro interior definido por \(x^2+y^2=\frac{1}{4}\) e o cone dado por $z^2=x^2+y^2$, intersectam-se sobre a circunferência definida por \(x^2+y^2=\frac{1}{4} \;;\; z = \frac{1}{2}\).

O cilindro exterior definido por $x^2+y^2=1$ e o cone dado por $z^2=x^2+y^2$, intersectam-se sobre a circunferência definida por \(x^2+y^2=\frac{1}{4} \;;\; z = 1\).

Portanto, há dois casos a considerar: um para \(0 \lt z \lt \frac{1}{2}\) e outro para \( \frac{1}{2}\lt z\lt 1\).

Alternativamente, note-se que se tem, simultaneamente,
$\frac{1}{4}<x^2+y^2$ \(\;;\;\) $z^2<x^2+y^2$.

Portanto, há dois casos a considerar: ou $z^2<\frac{1}{4}$, ou $z^2>\frac{1}{4}$.

Para o caso em que $0<z<\frac{1}{2}$, o corte correspondente é uma coroa circular, de raios \(\frac{1}{2}\) e \(1\), respectivamente, definida por $\frac{1}{4}<x^2+y^2<1$, tal como se mostra na figura seguinte:

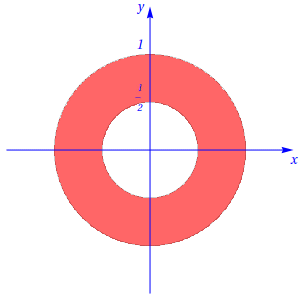
Para o caso em que $\frac{1}{2}<z<1$, o corte correspondente é uma coroa circular, de raios $z$ e $1$, respectivamente, definida por $z^2<x^2+y^2<1$, tal como se mostra na figura seguinte:

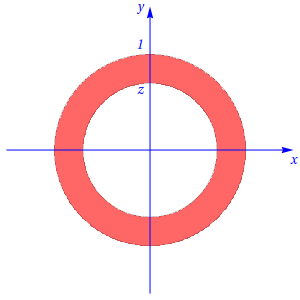
Cálculo do volume

Seja \(X\) o sólido e considerem-se os cortes \(C_1(z)\) e \(C_2(z)\), perpendiculares ao eixo \(Oz\): \[C_1(z)=\{(x,y): \, \frac 1 4 \lt x^2+y^2 \lt 1\}, \quad 0 \lt z \lt \frac{1}{2}.\] \[C_2(z)=\{(x,y): \, z^2 \lt x^2+y^2 \lt 1\}, \quad \frac{1}{2} \lt z \lt 1.\] Pelo Teorema de Fubini, tem-se \[\vol_3(X)=\int_{0}^{1/2} \vol_2(C_ 1(z))dz + \int_{1/2}^{1} \vol_2(C_ 2(z))dz.\]

O corte \(C_1(z)\) (Fig. 3) é uma coroa circular de raios \(\frac 1 2\) e \(1\), respectivamente. Portanto, \[\vol_2(C_1(z))=\pi (1-\frac 1 4)=\frac{3\pi}{4}.\]

O corte \(C_2(z)\) (Fig. 4) é uma coroa circular de raios \(z\) e \(1\), respectivamente. Portanto, \[\vol_2(C_2(z))=\pi(1-z^2).\] Assim, \[\begin{align}\vol_3(X) &=\int_{0}^{1/2}\frac{3\pi}{4}dz+\int_{1/2}^{1}\pi\left(1-z^2\right)dz \\ &=\frac{7\pi}{12}.\end{align}\]