\(x^2+y^2 \gt 1 \;;\; x^2+y^2+z^2 \lt 4 \)

Cortes perpendiculares ao eixo \(Ox\)

Da definição é claro que se tem \(-2 \lt x \lt 2\) e \[\begin{cases} y^2+z^2 \lt 4-x^2 \\ y^2 \gt 1-x^2. \end{cases}\] Sendo \(y^2 \geq 0\), há dois casos a considerar: um para \(|x| \lt 1\) e outro para \(1 \lt |x| \lt 2.\)

Assim, para o caso em que \(1 \lt |x| \lt 2\), tem-se \[y^2+z^2 \lt 4-x^2, \] e o corte correspondente é o círculo de raio \(\sqrt{4-x^2}\), tal como se mostra na figura seguinte:

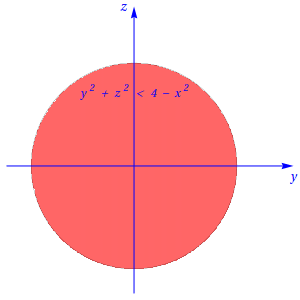
Para o caso em que \(|x| \lt 1\), tem-se \[\begin{cases} y^2+z^2 \lt 4-x^2 \\ |y| \gt \sqrt{1-x^2}, \end{cases}\] e o corte correspondente é o conjunto que se mostra na figura seguinte:

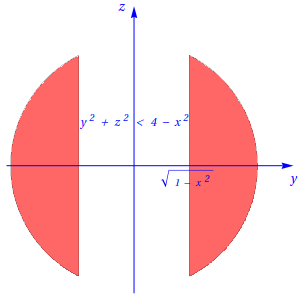
Cortes perpendiculares ao eixo \(Oz\)

Da definição é claro que se tem \[1 \lt x^2+y^2 \lt 4-z^2\] e, portanto, \[|z| \lt \sqrt{3}.\]

Assim, o corte correspondente é uma coroa circular de raios \(1\) e \(\sqrt{4-z^2},\) tal como se mostra na figura seguinte:

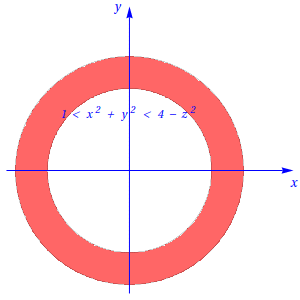
Cálculo do volume

Seja \(X\) o sólido e considerem-se os cortes \(C(z)\), perpendiculares ao eixo \(Oz\): \[C(z)=\left\{(x,y): \,1 \lt x^2+y^2 \lt 4-z^2 \right\}, \quad -\sqrt{3} \lt z \lt \sqrt{3}.\] Pelo Teorema de Fubini, tem-se \[\vol_3(X)=\int_{-\sqrt{3}}^{\sqrt{3}} \vol_2(C(z))dz.\] Dado que o corte \(C(z)\) é uma coroa circular, tal como se mostra na Fig. 3, então \[\vol_2(C(z))=\pi (4-z^2-1)=\pi (3-z^2)\] e, portanto, \[\vol_3(X)=2\pi\int_{0}^{\sqrt{3}} \left(3-z^2\right)dz= 4\pi\sqrt{3}.\]