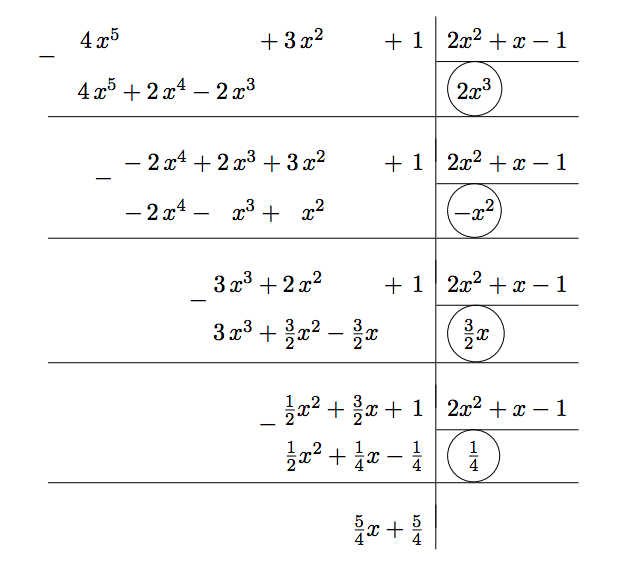Introdução à Programação em Python

(5) Exercícios sobre tipos de dados e programação em larga escala

Carlos Caleiro, Jaime Ramos

Dep. Matemática, IST - 2016

(versão de 8 de Fevereiro de 2019)

1 - Utilização de tipos de dados

1. Recorde o tipo de dados stack, definido no Notebook 08 - Programação em larga escala com as operações a seguir descritas:

  • new - a constante que denota a pilha nova vazia.
  • push(x,s) - a pilha que se obtém da pilha s sobrepondo-lhe o elemento x.
  • pop(s) - a pilha que se obtém da pilha s retirando-lhe o elemento no topo.
  • top(s) - o elemento que se encontra no topo da pilha s.
  • emptyQ(s) - True se s é a pilha vazia; False em caso contrário.

a) Sobre esta camada, defina as seguintes operações:

  1. mostra(s) - mostra o conteúdo da pilha s.
  2. soma(s) - recebe uma pilha de números naturais e devolve a soma dos seus elementos.
  3. inverte(s) - devolve uma pilha com os elementos de s por ordem inversa.
  4. noc(x,s) - devolve o número de ocorrências de x na pilha s.
  5. subpilhaQ(s1,s2) - devolve True se a pilha s1 for subpilha de s2, devolve False em caso contrário. Uma pilha s1 diz-se subpilha de uma pilha s2 se s2 é igual a s1 ou s2 pode ser obtida de s1 sobrepondo-lhe alguns elementos.
  6. sobrepoe(s1,s2) - devolve a pilha que se obtém de sobrepôr os elementos de s1 aos de s2, mantendo a ordem.

b) Importe o módulo stack, que se encontra disponível na página da cadeira e teste as operações para garantir que se comportam é como esperado.

c) Importe o módulo stack2 com uma implementação alternativa do tipo de dados pilha e volte a testar as operações, sem as alterar.

In [47]:
import stack
In [48]:
s1=stack.push(1,stack.push(2,stack.push(3,stack.new())))
In [50]:
mostra(s1)

1
2
3
In [52]:
soma(s1)
Out[52]:
6
In [45]:
s2 = inverte(s1)
In [46]:
mostra(s2)

3
2
1
In [48]:
noc(3,s1)
Out[48]:
1
In [54]:
s3= stack.push(2,stack.push(3,stack.new()))
In [55]:
subpilha(s3,s1)
Out[55]:
True
In [56]:
subpilha(s2,s1)
Out[56]:
False
In [63]:
mostra(s1)

1
2
3
In [67]:
s4=stack.push(8,stack.push(9,stack.new()))
In [68]:
mostra(s4)

8
9
In [69]:
s5=sobrepoe(s4,s1)
In [71]:
mostra(s5)

8
9
1
2
3
In [72]:
import stack2 as stack
In [73]:
s1=stack.push(1,stack.push(2,stack.push(3,stack.new())))
In [74]:
mostra(s1)

1
2
3
In [75]:
s2=inverte(s1)
In [76]:
mostra(s2)

3
2
1

2. Recorde o tipo de dados queue, definido no Notebook 08 - Programação em larga escala com as operações a seguir descritas:

  • newq - a constante que denota a fila nova vazia.
  • enter(x,f) - a fila que se obtém da fila f com a chegada do elemento x.
  • leave(f) - a fila que se obtém da fila f com a saída do primeiro elemento.
  • first(f) - o elemento que se encontra à frente da fila f.
  • emptyQ(f) - True se a fila s está vazia; False em caso contrário.

a) Sobre esta camada, defina as seguintes operações:

  1. mostra(f) - mostra o conteúdo da fila f.
  2. comprimento(f) - devolve o comprimento da fila f.
  3. distribui(f) - devolve duas filas f1 e f2, onde foram distribuidos alternadamente os elementos de f.
  4. prefixo(f1,f2) - devolve True se a fila f1 for prefixo da fila f2, e devolve False em caso contrário.
  5. subfila(f1,f2) - devolve True se a fila f1 for prefixo da fila f2, e devolve False em caso contrário. Uma fila f1 diz-se subfila de f2 se f1 é igual a f2 ou f2 pode ser obtida de f1 acrescentando-lhe alguns elementos no ínicio e outros no fim

b) Importe o módulo myqueue, que se encontra disponível na página da cadeira e teste as operações para garantir que se comportam como é esperado.

In [77]:
import myqueue as queue
In [104]:
f = queue.enter(5,queue.enter(7,queue.enter(3,queue.enter(2,queue.enter(4,queue.newq())))))
In [106]:
mostra(f)

[4, 2, 3, 7, 5]
In [108]:
comprimento(f)
Out[108]:
5
In [110]:
f1,f2=distribui(f)
In [111]:
mostra(f1)

[4, 3, 5]
In [112]:
mostra(f2)

[2, 7]
In [116]:
prefixo(f1,f)
Out[116]:
False
In [117]:
prefixo(f1,f1)
Out[117]:
True
In [119]:
mostra(f)

[4, 2, 3, 7, 5]
In [120]:
f3 = queue.enter(7,queue.enter(3,queue.enter(2,queue.newq())))
In [122]:
subfila(f3,f)
Out[122]:
True
In [123]:
subfila(f1,f)
Out[123]:
False

3. Considere o tipo de dados fset, dos conjuntos finitos de números inteiros, munido das seguintes operações:

  • emptyset() - constante que denota o conjunto vazio.
  • insert(x,s) - acrescenta o elemento x ao conjunto s.
  • remove(x,s) - retira o elemento x do conjutno s.
  • emptyQ(s) - True se s é o conjunto vazio; False em caso contrário.
  • memberQ(x,s) - True se x é elemento do conjunto s; False em caso contrário.
  • infm(s) - ínfimo do conjunto s.
  • sup(s) - supremo do conjunto s.
  • card(s) - cardinal de s.
  • show(s) - mostra o conteúdo do conjunto s.

a) Sobre esta camada, defina as seguintes operações:

  1. union(s1,s2) - operação que calcula a união dos conjuntos s1 e s2.
  2. intersect(s1,s2) - operação que calcula a intersecção dos conjuntos s1 e s2.
  3. subset(s1,s2) - operação que devolve True se s1 é subconjunto de s2.

b) Importe o módulo fset, que se encontra disponível na página da cadeira e teste as operações para garantir que se comportam como é esperado.

In [2]:
import fset
In [5]:
s1 = fset.insert(1,fset.insert(2,fset.insert(1,fset.emptyset())))
In [6]:
s2 = fset.insert(1,fset.insert(2,fset.insert(3,fset.emptyset())))
In [31]:
fset.show(s1)

[1, 2]
In [34]:
s3=union(s1,s2)
In [35]:
fset.show(s3)

[1, 2, 3]
In [42]:
s4=intersect(s1,s2)
In [44]:
fset.show(s4)

[1, 2]
In [7]:
subset(s1,s2)
Out[7]:
True
In [8]:
subset(s2,s1)
Out[8]:
False

4. Um saco ou multiconjunto é um conjunto em que os elementos podem aparecer repetidos. É importante saber quantas vezes é que um elemento está repetido num saco. Considere o tipo de dados fbag, dos sacos finitos de números inteiros, munido das seguintes operações:

  • newbag() - representa o multiconjunto vazio.
  • insert(x,s) - acrescenta uma cópia de x ao multiconjunto s.
  • remove(x,s) - retira uma cópia de x ao multiconjunto s, retornando s se x não pertencer a s.
  • removeall(x,s) - retira todas as cópias de x ao multiconjunto s, retornando s se x não pertencer a s.
  • card(s) - devolve o número de elementos em s.
  • ncopies(x,s) - devolve o número de cópias de x em s.
  • nelem(s) - devolve o número de elementos distintos em s.
  • emptyQ(s) - devolve True se s for o multiconjunto vazio e False caso contrário.
  • memberQ(x,s) - devolve True se existir pelo menos uma cópia de x em s e False em caso contrário.
  • infm(s) - ínfimo de s.
  • sup(s) - supremo de s.
  • show(s) - mostra o conteúdo do conjunto s.

a) Sobre esta camada, defina as seguintes operações:

  1. union(s1,s2) - operação que calcula a união dos sacos s1 e s2.
  2. maioritarios(s) - operação que devolve a lista dos elementos que ocorrem mais vezes no saco s.

b) Importe o módulo fbag, que se encontra disponível na página da cadeira e teste as operações para garantir que se comportam como é esperado.

In [53]:
import fbag
In [55]:
s1=fbag.insert(1,fbag.insert(2,fbag.insert(1,fbag.insert(3,fbag.insert(1,fbag.insert(4,fbag.newbag()))))))
In [56]:
fbag.show(s1)

[1, 1, 1, 2, 3, 4]
In [63]:
s2=fbag.insert(3,fbag.insert(2,fbag.insert(5,fbag.insert(5,fbag.insert(5,fbag.insert(3,fbag.newbag()))))))
In [64]:
fbag.show(s2)

[2, 3, 3, 5, 5, 5]
In [66]:
union(s1,s2)
Out[66]:
[1, 1, 1, 2, 2, 3, 3, 3, 4, 5, 5, 5]
In [71]:
maioritarios(union(s1,s2))
Out[71]:
[1, 3, 5]

5. Uma árvore de pesquisa de registos é uma árvore binária em que cada nó é um registo. No que se segue, vamos assumir que um registo é um par constituido por um número natural (a chave do registo), relevante para a ordenação, e pelo seu conteúdo (um elemento de tipo arbitrário R). As operações seguintes permitem manipular árvores binárias de registos:

  • emptyreg() - representa a árvore vazia.
  • treereg(t1,k,d,t2) - devolve a árvore binária com registo de conteúdo d e chave k na raíz, subárvore esquerda t1 e subárvore direita t2.
  • labelreg(t) - devolve o conteúdo do registo na raíz da árvore t.
  • leftreg(t) - devolve a subárvore esquerda de t.
  • rightreg(t) - devolve a subárvore direita de t.
  • emptyQreg(t) - devolve True se t for a árvore vazia, devolve False em caso contrário.
  • keysearchQreg(k,t) - devolve True se existir em t um registo com chave k, devolve False em caso contrário.
  • keyFindQreg(k,t) - devolve o conteúdo do registo associado à chave k em t (não está definida se não existir registo com chave k na árvore).
  • insertreg(k,d,t) - devolve a árvore que se obtém de t acrescentando-lhe um registo com chave k e conteúdo d.
  • deltreg(k,t) - devolve a árvore que se obtém de t apagando-lhe um registo com chave k. No caso não existir nehum registo com chave k, devolve a árvore t inalterada.

a) Sobre esta camada, defina as seguintes operações:

  1. listareg(t) - operação que devolve a lista dos conteúdos dos registos de t, ordenada por chave.
  2. registosQ(t,w) - operação verifica se todas as chaves em w ocorrem na árvore t.
  3. registos(t,w) - operação que devolve a lista dos conteúdos dos registos em t correspondentes às chaves em w.

b) Importe o módulo searchbintreereg, que se encontra disponível na página da cadeira e teste as operações para garantir que se comportam como é esperado.

In [3]:
import searchbintreereg as tree
In [50]:
t1=tree.insertreg(2,'e',tree.insertreg(1,'d',tree.insertreg(7,'c',tree.insertreg(3,'b',tree.insertreg(5,'a',tree.emptyreg())))))
In [9]:
tree.labelreg(t1)
Out[9]:
'a'
In [10]:
tree.labelreg(tree.leftreg(t1))
Out[10]:
'e'
In [11]:
tree.labelreg(tree.rightreg(t1))
Out[11]:
'c'
In [13]:
listareg(t1)
Out[13]:
['d', 'e', 'b', 'a', 'c']
In [18]:
registosQ(t1,[1,2,4])
Out[18]:
False
In [19]:
registosQ(t1,[1,2,3])
Out[19]:
True
In [23]:
registos(t1,[1,2,3])
Out[23]:
['d', 'e', 'b']
In [24]:
registos(t1,[4,5,6])

Erro! A chave 4 não está presente na árvore.

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-24-6539796c8388> in <module>()
----> 1 registos(t1,[4,5,6])

<ipython-input-22-12985d441a81> in registos(t, w)
      4     elif not tree.keysearchQreg(w[0],t):
      5         print('Erro! A chave',w[0],'não está presente na árvore.')
----> 6         assert(tree.keyFindQreg(w[0],t))
      7     else:
      8         return [tree.keyFindQreg(w[0],t)]+registos(t,w[1:])

AssertionError:

6. Considere os módulos stack e tree descritos acima. Sobre esta camada, defina as seguintes operações:

  • fazarvore(s) - recebe uma pilha de pilhas de números naturais e devolve a árvore de pesquisa de registos contento essas mesmas pilhas; a chave associada a cada pilha é a soma dos seus elementos.
  • geraarvore(s1,s2) - recebe como argumento duas pilhas s1 e s2 de números naturas com a mesma profundidade e devolve a árvore de pesquisa de registos que se obtém considerando que cada elemento de s1 é o conteúdo de um registo cuja chave é o elemento correspondente da pilha s2. Ignore elementos que sobrem em qualquer uma das pilhas.
  • gerapilha(t) - recebe como argumento uma árvore pesquisa de registos cujos conteúdos são números naturais e devolve a pilha dos conteúdos dos registos que ocorrem na árvore , ordenados pela sua chave (com o registo com menor chave no fundo da pilha).
In [27]:
import searchbintreereg as tree
import stack
In [29]:
p1 = stack.push(2,stack.push(1,stack.new()))
In [30]:
stack.top(p1)
Out[30]:
2
In [31]:
p2 = stack.push(5,stack.new())
In [32]:
p3 = stack.push(4,stack.push(0,stack.new()))
In [33]:
p = stack.push(p1,stack.push(p2,stack.push(p3,stack.new())))
In [34]:
stack.top(stack.top(p))
Out[34]:
2
In [37]:
t = fazarvore(p)
In [38]:
stack.top(tree.keyFindQreg(3,t))
Out[38]:
2
In [39]:
stack.emptyQ(stack.pop(tree.keyFindQreg(5,t)))
Out[39]:
True
In [41]:
q1=stack.push(2,stack.push(3,stack.push(5,stack.new())))
In [42]:
q2=stack.push(4,stack.push(0,stack.push(2,stack.new())))
In [43]:
t2=geraarvore(q1,q2)
In [45]:
tree.keyFindQreg(4,t2)
Out[45]:
2
In [46]:
tree.keyFindQreg(0,t2)
Out[46]:
3
In [47]:
tree.keyFindQreg(2,t2)
Out[47]:
5
In [64]:
mostra(gerapilha(t1))

c
a
b
e
d

Desenvolvimento de módulos

No contexto da programação em grande escala, é importante saber desenvolver e utilizar módulos. Existem inúmeras alternativas para criar, alterar e manipular módulos. Uma dessas alternativas é a utilização do IDE Spyder, que a seguir se ilustra. Comece por iniciar a aplicação Spyder. Abre-se uma janela subdividida em 3 janelas. A janela do lado esquerdo é a janela de edição de código. É onde vamos editar os nossos módulos. Funciona como um editor de texto normal mas reconhece reconhece a estrutura do código Python, usando um código de cores para facilitar a leitura dos programas. Dispõe também de um corrector de sintaxe que nos dá indicações sobre possíveis erros de sintaxe que possamos estar a cometer mesmo antes de executar o programa. Do lado direito, há duas duas janelas. janela superior, denominada Variable explorer mantem actualizada a informação sobre as variáveis que vão sendo usadas durante cada sessão. A janela inferior, denomindada IPython console, disponibiliza um interface com o IPython, que nos permite interagir com o programa (de forma interactiva). Para o programa ficar disponível no ambiente interactivo é necessário executá-lo. A maneira mais expedita de o fazer é clicando na seta verde que se encontra na barra de ferramentas no topo da janela. O ambiente interactivo continua a disponiblizar todas as funcionalidades do IPython que temos vindo a usar nos notebooks Jupyter.

Abra o módulo stack e acrescente-lhe a operação depth que calcula a profundidade de uma pilha. Teste as diversas operações deste módulo na consola.

2 - Implementação de tipos de dados abstractos

1. Recorde o tipo de dados stack.

a) Defina um módulo com uma implementação alternativa para este tipo de dados em que uma pilha é representada por uma lista em que o elemento no topo da pilha é o elemento mais à direita da lista.

b) Volte a testar as operações que definiu em 1 e confirme que funcionam correctamente.

c) Enriqueça o módulo com as operações soma, noc, inverte, subpilha e sobrepoe, descritas em 1, tirando partido da implementação.

2. Recorde o tipo de dados fbag.

a) Defina um módulo com uma implementação para este tipo de dados adoptando a seguinte representanção: um saco é representado por uma lista de pares (n,r) em que n é um elemento do saco e r é o número de vezes que esse elemento aparece repetido no saco (com r>0).

b) Volte a testar as operações que definiu em 1 e confirme que funcionam correctamente.

c) Enriqueça o módulo com as operações union, intersect e maioritarios, descritas em 1, tirando partido da implementação.

3. Considere o tipo de dados fila de espera com prioridades em que certos elementos podem entrar na fila com prioridade. Cada elemento ao entrar na fila, se tiver prioridade, passa à frente de todos os elementos sem prioridade, mas fica atrás dos elementos que também têm prioridade; se não tiver prioridade fica no fim da fila. A prioridade é um valor lógico. Considere as operações:

  • newq - a constante que denota a fila nova vazia.
  • enter(x,f,p) - a fila que se obtém da fila f com a chegada do elemento x, e com prioridade determinada por p.
  • leave(f) - a fila que se obtém da fila f com a saída do primeiro elemento.
  • first(f) - o elemento que se encontra à frente da fila f.
  • priorityQ(f) - devolve True se o primeiro elemento da fila tem prioridade e False em caso contrário.
  • howmanyP(f) - devolve o número de elementos na fila f que têm prioridade.
  • howmanyNP(f) - devolve o número de elementos na fila f que não têm prioridade.
  • emptyQ(f) - True se a fila s está vazia; False em caso contrário.

a) Defina um módulo pqueue com uma implementação deste tipo de dados. Escolha a repreentação que achar mais conveniente.

b) Enriqueça o tipo de dados anterior, assumindo que a prioridade passa a ser um número natural tal que quanto menor for esse número maior é a prioridade.

In [70]:
import pqueue
In [71]:
f = pqueue.enter(3,pqueue.enter(1,pqueue.newq(),False),False)
In [72]:
pqueue.first(f)
Out[72]:
1
In [74]:
f = pqueue.enter(2,f,True)
In [75]:
pqueue.first(f)
Out[75]:
2
In [76]:
pqueue.howmanyP(f)
Out[76]:
1
In [77]:
pqueue.howmanyNP(f)
Out[77]:
2
In [78]:
pqueue.priorityQ(f)
Out[78]:
True
In [79]:
f = pqueue.leave(f)
In [80]:
pqueue.first(f)
Out[80]:
1
In [81]:
pqueue.howmanyP(f)
Out[81]:
0
In [82]:
pqueue.priorityQ(f)
Out[82]:
False

4. Um grafo dirigido é um par $(V,A)$, onde $V$ é um conjunto (de vértices) e $A$ é um conjunto (de arestas) de pares de elementos de $V$. Quando o par $(v_1,v_2)$ é um aresta, dizemos que $v_1$ e $v_2$ estão ligados ou que há um caminho de $v_1$ para $v_2$. O facto de o grafo ser dirigido significa que a existência de um caminho de $v_1$ para $v_2$ é independente da existência de um caminho de $v_2$ para $v_1$. Considere as operações seguintes sobre o tipo da dados grafo dirigido:

  • newgraph(N) - representa o grafo vazio com vértices {1,...,N}.
  • addedge(g,x,y) - representa o grafo que se obtém acrescentando uma aresta de x para y ao grafo g.
  • deledge(g,x,y) - representa o grafo que se obtém retirando a aresta de x para y ao grafo g, caso esta exista (devolvendo g caso contrário).
  • dim(g) - devolve o número de vértices de g.
  • graphQ(e) - devolve True se e representar um grafo e False em caso contrário.
  • emptyQ(g) - devolve True se g for o grafo vazio.
  • edge(g,x,y) - devolve True se houver uma aresta de x para y no grafo g.

a) Desenvolva um módulo graph1 com uma implementação para o tipo de dados grafo dirigido adoptando a seguinte representação: um grafo é representado por uma lista de pares (N,w) em que N é o número de vértices e w é a lista das arestas do grafo.

b) Desenvolva um módulo graph2 com uma implementação para o tipo de dados grafo dirigido adoptando a seguinte representação: um grafo com N vértices é representado por uma lista de listas [w1,...,wN] em que wi é a lista dos sucessores directo do vértice i.

c) Desenvolva um módulo graph3 com uma implementação para o tipo de dados grafo dirigido adoptando a seguinte representação: um grafo com N vértices é representado por uma matriz quadrada m de dimensão N em que m[i][j]=1 se existe uma aresta do vértice i para o vértice j, e m[i][j]=0 em caso contrário (matriz de adjacência).

d) Sobre a camada dos grafos, defina as operações a seguir descritas e teste-as com cada uma das implementações anteriores:

  • pathQ(g,w) - recebe um grafo g e uma sequência de vértices w e verifica se w constitui um caminho (sequência de arestas) em g.
  • addpath(g,w): recebe um grafo g e um caminho w e acrescenta esse caminho a g (aresta a aresta).
  • sucs(g,v) - recebe um grafo g e um vértice v e devolve a lista dos sucessores imediatos de v.
  • ligados(g,v1,v2) - recebe como argumentos um grafo g e dois vértices v1 e v2 e devolve True se os vértices v1 e v2 estiverem ligados por um caminho em g e devolve False em caso contrário.
  • acessiveis(g,v) - recebe um grafo g e um vértice v e devolve a lista dos vértices acessíveis a partir de v (em qualquer número de passos).
  • fecho(g): recebe um grafo g e devolve o grafo cujas arestas são os caminhos de g.
  • custo(g,w,f) - recebe um grafo g, um caminho w e uma função (de custo) f sobre pares de naturais e devolve o custo do caminho.
  • completo(n) - recebe um natural n e devolve o grafo completo com vértices 0,...,n.
  • simetrico(g) - recebe um grafo g e devolve o grafo simétrico de g.
  • fechosim(g) - recebe um grafo g e devolve o grafo simétrico que se obtém de g acrescentando a aresta de v2 para v1 sempre que haja um caminho de v1 para v2 em g.

3 - Implementação de tipos de dados usando classes

Desenvolva implementações para os tipos de dados anteriores recorrendo a classes, mantendo a representação sempre que possível e fazendo as necessárias adaptações.

4 - Exercícios complementares

1. Considere filas de espera com prioridades, em que cada elemento entra na fila com uma dada prioridade (um número inteiro) que lhe permite sair antes de todos os elementos da fila com prioridade inferior, com as seguintes operações:

  • vazia(): fila vazia;
  • entra(f,x,q): fila que resulta da entrada na fila f do elemento x com prioridade p;
  • prox(f): próximo elemento que sairá da fila f;
  • sai(f): fila que resulta da saída do próximo elemento de f;
  • compr(f): número de elementos da fila f;
  • fpbfQ(e): True se e só se e é uma fila com prioridade bem formada.

Por exemplo, deverá ter-se prox(entra(entra(vazia(),x,1),y,1)) igual a x, mas prox(entra(entra(vazia(),x,1),y,2)) igual a y.

a) Desenvolva em Python uma implementação eficiente deste tipo de dados, de modo a que cada fila com prioridades seja representada por uma lista da forma $[({\tt x}_{\tt 1},{\tt p}_{\tt 1}),...({\tt x}_{\tt n},{\tt p}_{\tt n})]$ onde os elementos surgem por ordem de entrada, isto é, cada ${\tt x}_{\tt i}$ é o ${\tt i}$-ésimo elemento que entrou da fila e ${\tt p}_{\tt i}$ a sua prioridade.

b) Desenvolva em Python, sobre a camada de abstracção acima desenvolvida e assegurando independência da implementação, uma função ordena que recebendo uma lista números inteiros a devolve oredenada por ordem crescente (construindo uma fila de espera com prioridades adequadas).

2. Considere filas de espera com prioridade e tolerâncias, em que cada elemento entra na fila com uma dada prioridade e tolerância (inteiros positivos). A prioridade permite que o elemento ultrapasse na fila todos os elementos com prioridade inferior. A tolerância decrementa sempre que sai um elemento da fila e faz com que o elemento abandone a fila ao chegar a 0. Identificaram-se as seguintes operações:

  • vazia: fila vazia;
  • entra(f,x,p,t): fila que resulta da entrada na fila f do elemento x com prioridade p e tolerância t;
  • prox(f): elemento que está no início da fila f;
  • sai(f): fila que resulta da saída do próximo elemento de f;
  • compr(f): número de elementos de f;
  • fptbfQ(e): True se e só se e é uma fila de espera com prioridades e tolerâncias bem formada.

Note, por exemplo, que deve ser c o resultado de:

prox(sai(entra(entra(entra(vazia(),c,1,10),b,4,1),a,5,3))).

a) Desenvolva em Python uma implementação eficiente deste tipo de dados, de modo a que cada fila com prioridades e tolerâncias seja representada por uma lista da forma $[({\tt x}_{\tt 1},{\tt p}_{\tt 1},{\tt t}_{\tt 1}),...({\tt x}_{\tt n},{\tt p}_{\tt n},{\tt t}_{\tt n})]$ onde os elementos surgem por ordem de saída, isto é, cada ${\tt x}_{\tt i}$ é o ${\tt i}$-ésimo elemento que sairá da fila (se a sua tolerância ${\tt t}_{\tt i}$ o permitir).

b) Desenvolva em Python, sobre a camada de abstracção acima desenvolvida e assegurando a independência da implementação, uma função maxprioque recebendo uma fila de espera com prioridades e tolerâncias não vazia f calcula a prioridade máxima de algum elemento na fila f (pode assumir que os elementos na fila são ${\tt 1}, {\tt 2}, {\tt 3}..., {\tt n}$ onde ${\tt n}$ é o seu comprimento).

3. Considere o tipo de dados tape que consiste de uma fita de memória infinita dividida em células, onde cada célula pode conter um símbolo (no exemplo temos 0,1 e células vazias), equipada com uma cabeça de leitura/escrita (cuja posição é indicada na figura pela célula sombreada).

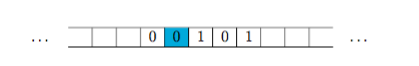
Drawing

Identificaram-se as seguintes operações:

  • new(): tape vazia (todas as células estão vazias);
  • left(t): tape que resulta de t movendo a cabeça de leitura/escrita para célula imediatamente à esquerda;
  • right(t): tape que resulta de t movendo a cabeça de leitura/escrita para célula imediatamente à direita;
  • blankQ(t): True se e só se está vazia a célula de memória onde está posicionada a cabeça de leitura/escrita de t;
  • read(t): símbolo que está em t na célula de memória onde está posicionada a cabeça de leitura/escrita;
  • write(t,s): tape que resulta de t escrevendo o símbolo s na célula de memória onde está posicionada a cabeça de leitura/escrita;
  • tbfQ(e): True se e só se e é uma tape bem formada.

Por exemplo, sendo t a tape indicada acima, left(write(left(t),1)) deverá resultar na tape

Drawing

a) Desenvolva em Python uma implementação eficiente deste tipo de dados, de modo a que cada tape seja representada por uma lista da forma $[{\tt p},({\tt p}_{\tt 1},{\tt t}_{\tt 1}),...,({\tt p}_{\tt n},{\tt t}_{\tt n})]$ onde ${\tt p}$ é um inteiro que identifica a posição actual da cabeça de leitura/escrita, cada ${\tt p}_{\tt i}$ é um inteiro que identifica a posição de uma célula não vazia e ${\tt s}_{\tt i}$ é o símbolo nela inscrito. Convenciona-se que as células são numeradas sequencialmente e que 0 corresponde à posição original da cabeça de leitura/escrita no momento de criação da tape.

b) Desenvolva em Python, sobre a camada de abstracção acima desenvolvida e assegurando independência da implementação, uma função double que, recebendo uma tape cuja cabeça de leitura/escrita está colocada na célula mais à esquerda de uma sequência finita de 1s (com todas as outras células vazias), devolve a tape alterada por forma a que no final a sua cabeça de leitura/escrita esteja colocada na célula mais à esquerda de uma sequência de 1s com o dobro do tamanho.

4. A árvore binária desenhada abaixo tem os nós numerados sequencialmente, de cima para baixo e da esquerda para a direita (cada $n_i$ é o valor contido no nó $i$). Como em qualquer árvore binária, cada nó pai (num certo nível da árvore) tem no máximo dois nós filhos (no nível imediatamente abaixo). Por exemplo, o nó 1 tem como filhos os nós 3 e 4. O nó 5 tem apenas um filho,o nó 11. O nó 11, por sua vez, não tem filhos. A árvore acima diz-se completa pois todos os seus níveis estão completamente preenchidos, possivelmente à excepção do último, e nesse último nível os nós ocupados estão encostados à esquerda. O próximo nó disponível na árvore corresponderia ao nó 12, o filho mais à direita do nó 5; depois os dois nós filhos do nó 6; e a seguir os filhos do nó 7, etc.
Considere o tipo de dados árvore binária completa de inteiros, em que os nós contêm números inteiros, com as seguintes operações:

  • void(): árvore vazia;
  • add(t,n): árvore que resulta de adicionar o inteiro n no próximo nó disponível da árvore t;
  • val(t,i): valor contido no nó i da árvore t;
  • swap(t,i): árvore que resulta da árvore t trocando o valor contido no nó i com o valor do seu pai;
  • size(t): número de nós da árvore t;
  • heapQ(t): True se e só se a árvore binária completa de inteiros t é uma heap, isto é, se cada nó contém um valor maior ou igual que os valores contidos nos seus filhos.

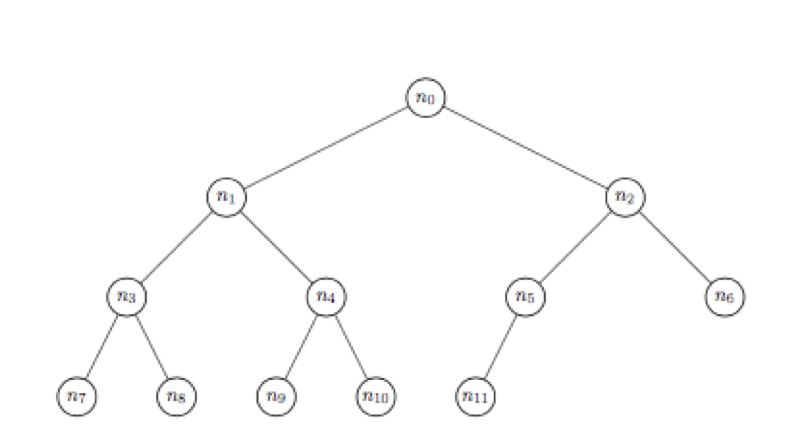
Drawing

a) Desenvolva em Python uma implementação eficiente deste tipo de dados, de modo a que cada árvore binária completa de inteiros seja representada simplesmente por uma lista da forma ${\tt [n_0,n_1,n_2,...,n_{k−1}]}$ onde ${\tt k}$ é o número de nós da árvore, e cada ${\tt n_i}$ é o valor contido no nó ${\tt i}$.

b) Desenvolva em Python, sobre a camada de abstracção acima desenvolvida e assegurando a independência da implementação, uma função siftUP que, recebendo uma heap t e um inteiro n devolve uma heap com todos os valores dos nós de t e um nó adicional com o valor n. Sugestão: adicione n no fundo de t e use a operação swap para manipular a árvore obtida de forma a garantir a propriedade de heap.

5. Considere bitmaps (figuras rectangulares, com pixels a preto-e-branco) e filmes (sequências de bitmaps com as mesmas dimensões) com as operações:

  • white(n,m): bitmap com $n$ linhas e $m$ colunas e todos os pixels em branco;
  • pixflip(b,w): bitmap que resulta de trocar a cor dos pixels do bitmap b nas posições correspondentes à linha i coluna j para cada par (i,j) que ocorre na linha w;
  • isblack(b,i,j): True se é preto o pixel correspondente à linha i coluna j do bitmap b, e False caso contrário;
  • compose(b1,b2): bitmap em que cada pixal do bitmap b1 passa a ter as dimensões do bitmap b2, ficando em branco se o pixel de b1 está em branco, ou contendo cópia de b2 se o pixel de b1está a preto (ver figura);
  • start(b): filme cujo primeiro é único bitmap é b;
  • append(f,b): filme que resulta de juntar o bitmap b no final do filme f;
  • size(f): número de bitmaps do filme f;
  • last(f): último frame do filme f;
  • endat(f,k): filme com apenas os primeiros k bitmaps do filme f.

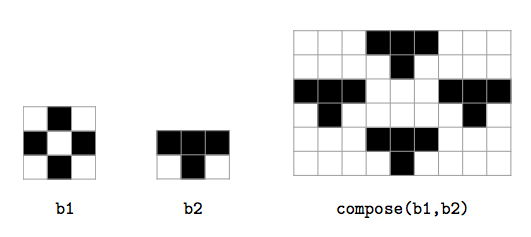
Drawing

a) Em Python, pretende-se representar cada bitmap como uma matriz de entradas 0,1 (0 para pixels a branco e 1 para pixels a preto), e representar cada filme como um para da forma (b,[(d1,...,dk]) onde b é o primeiro bitmap do filme, d1 é a lista das posições que é necessário trocar no primeiro bitmap do filme para obter o segundo bitmap, d2 é a lista das posições que é necessário trocar no segundo bitmap do filme para obter o terceiro, e assim por diante. Apresente implementações eficientes para as operações identificadas.

b)Desenvolva, sobre a camada de abstracção obtida acima e assegurando independência da implementação, as seguintes funções:

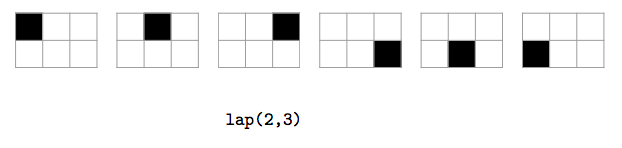
1) lap, que recebendo inteiros positivos n,m devolve o filme que resulta de, começando no canto superior esquerdo e sem repetir bitmaps, fazer circular um pixel preto na moldura de um bitmap branco com n linhas e m colunas no sentido dos ponteiros do relógio;

Drawing

2) makemovie, que recendo um natural t devolve o filme que correspondente à sequência de bitmaps da figura abaixo (com 1 volta), mas completando tvoltas.
Sugestão: use a função lapcomo auxiliar, mesmo se não a definiu.

Drawing

6. Considere polinómios (numa variável) com as seguintes operações:

  • mono(a,n): polinómios apenas com o monómio ${\tt a}x^{\tt n}$;
  • sum(p,q): soma s dos polinómios p,q, ou seja, ${\tt s}(x)={\tt p}(x)+{\tt q}(x)$;
  • prod(p,q): produto r dos polinómios p,q, ou seja, ${\tt r}(x)={\tt p}(x)+{\tt q}(x)$;
  • comp(p,q): composição t dos polinómios p,q, ou seja, ${\tt t}(x)={\tt p}({\tt q}(x))$;
  • degree(p): grau do polinómio p;
  • maincoef(p): coeficiente do monómio de maior grau do polinómio p;
  • zeroQ(p): True se o polinómio p é numo, e False em caso contrário;
  • eval(p,a): valor do polinómio p no ponto $x={\tt a}$, ou seja, ${\tt p}({\tt a})$.

Em Python, preetende-se representar cada polinómio de grau n como a lista de coeficiente dos seus monómios por ordem decrescente de grau. Nomeadamente, um polinómio da forma ${\tt a}_{\tt n}x^{\\ n}+{\tt a}_{\tt n-1}x^{\\ n-1}+...+{\tt a}_{\tt 2}x^{\\ 2}+{\tt a}_{\tt 1}x^{\\ 1}+{\tt a}_{\tt 0}$ deve coresponder à lista ${\tt [}{\tt a}_{\tt n},{\tt a}_{\tt n-1},...,{\tt a}_{\tt 2},{\tt a}_{\tt 1},{\tt a}_{\tt 0}{\tt ]}$, garantindo-se que ${\tt a}_{\tt n}\neq 0$ a menos que ${\tt n}=0$ e o polinómio seja nulo.

a) Apresente implementações eficientes para as operações identificadas.

b) Desenvolva, sobre a camada de abstracção obtida acima e assegurando a indenpendência da implementação, as seguintes funções:

b1) derivative, que dado um polinómio p devolve o polinómio d correspondente à sua derivada, i.e., ${\tt d}(x)={\tt p}'(x)$;

b2) division, que dados dois polinómios p,q devolve o par (d,r) tal que ${\tt d}(x)$ é o quociente da divisão de ${\tt p}(x)$ por ${\tt q}(x)$, e ${\tt r}(x)$ é o resto da divisão.
A figura ilustra a divisão de ${\tt p}(x)=4x^5+3x^2+1$ por ${\tt q}(x)=2x^3+x-1$. O quociente da divisão é ${\tt d}(x)=2x^3-x^2+\frac{3}{2}x+\frac{1}{4}$ e ${\tt r}(x)=\frac{5}{4}x+\frac{5}{4}$. Como seria de esperar, tem-se ${\tt p}(x)={\tt q}(x)\times{\tt d}(x)+{\tt r}(x)$. A dicisão é obtida subtraindo repetidamente ao dividendo (${\tt p}(x)$, ou que dele restar), o produto do divisor ${\tt q}(x)$ por um monómio escolhido de forma a igualar o monómio de maior grau de ambos. O processo termina quando o grau do dividendo é inferior ao grau do divisor, caso em que o dividendo se denomina o resto da divisão. O quociente da divisão obtém-se somando os vários monómios usados ao londo da divisão (dentro de círculos, na figura).

Drawing