Métodos Directos - Sistemas Lineares

Método de Eliminação de Gauss

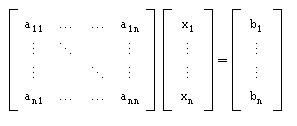
Consideremos o sistema Ax=b em que A é uma matriz quadrada n x n.

Objectivo do Método: Eliminar os elementos a_ij de forma a obter um sistema equivalente com uma matriz triangular superior. Depois bastará usar substituições sucessivas para chegarmos à solução pretendida.

O método consiste em n-1 passos, onde construimos elementos a^(k+1)_ij a partir dos elementos a^(k)_ij considerando como [a⁽¹⁾_ij] a matriz inicial.

PASSO k

(para k=1,... n-1)

Se o pivot a^(k)_kk=0 então há que efectuar troca de linhas.
Se a^(k)_kk=/= 0 calculamos

m_ik=a^(k)_ik / a^(k)_kk	i = k+1,... ,n
a^(k+1)_ij=a^(k)_ij - m_ika^(k)_kj	i, j = k+1, ..., n
b^(k+1)_i=b^(k)_i - m_ikb^(k)_k	i = k+1, ..., n

No final dos n-1 passos obtemos o sistema triangular superior equivalente:

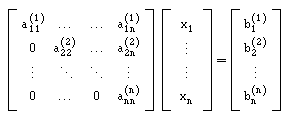
que se pode resolver facilmente por substituição ascendente:

Armazenando os coeficientes m_ik podemos obter uma factorização da matriz A na forma:

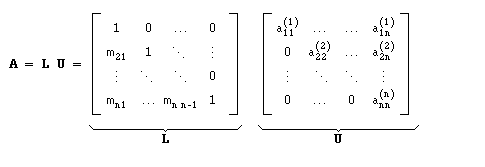
caso não sejam efectuadas trocas de linhas.

Caso existam trocas de linhas, a factorização é da forma P A = L U em que P é uma matriz de permutação. Ao resolver o sistema obteriamos

L U x = P b

Teorema II.1.1 :
A factorização A = L U em que

L é uma matriz triangular inferior com diagonal principal unitária

U é uma matriz triangular superior
é obtida de forma única se os pivots verificarem a^(k)_kk =/= 0.

Número de Operações

Analisemos agora qual o número de operações ( + - ou * / ) envolvido na resolução de um sistema:

FACTORIZAÇÃO da MATRIZ

Em cada Passo k :

Cálculo dos m_ik
n-k divisões --- correspondentes a um total de ( n - k ) operações.
Cálculo dos a_ij
( n - k )² multiplicações e subtracções--- correspondentes a um total de ( n - k )² operações.

CÁLCULO de b⁽ⁿ⁾

Em cada Passo k :

n - k multiplicações e subtracções correspondentes a um total de ( n - k ) operações.

SUBSTITUIÇÃO

No total teremos :
n + k = n (n + 1) / 2 multiplicações e divisões k = n(n - 1) / 2 subtracções

Como ( n - k ) = n (n - 1) / 2 e também ( n - k )² = n (n - 1) (2 n - 1) / 6 .

Obtemos a seguinte tabela :

.	Somas + Subtracções	Multipl. + Divisões
Factorização	n ( n - 1) ( 2 n -1) / 6	n ( n² - 1) / 3
Cálculo de b⁽ⁿ⁾	n ( n - 1 ) / 2	n ( n - 1 ) / 2
Substituição	n ( n + 1 ) / 2	n ( n - 1 ) / 2
TOTAL	~ n³ / 3	~ n³ / 3

é fácil ver que a sucessão o número total de operações, ao considerarmos uma dimensão da matriz elevada é assimptoticamente equivalente a 2 n³ / 3.

Este valor é bastante reduzido se comparado com o número de operações que seria necessário efectuar se resolvessemos o sistema pela Regra de Cramer (nesse caso teriamos ~ (n+1) ! operações, o que por exemplo, para n = 10 corresponderia a efectuar ~ 40 000 000 de operações ( * , / ) ao invés de ~ 430 pelo Método de Gauss ).

Pesquisa de Pivot

Tal como quando o pivot é nulo ( isto é a^(k)_kk=0 ) devemos efectuar uma troca de linhas, se o seu valor fôr próximo de zero, se não fôr efectuada uma troca de linhas ou colunas, os erros de arredondamento (ao ser originada a factorização da matriz), podem provocar grandes erros nos resultados.
Isto também acontece se houver um grande desiquilibrio de grandezas nos elementos da matriz -- muito maiores face ao pivot (o que é equivalente, dividindo, a que ele seja próximo de zero).

Para contornar este problema de estabilidade numérica, usam-se as seguintes estratégias:

PESQUISA PARCIAL DE PIVOT : (normalmente por linhas)
Em cada Passo k da eliminação de Gauss, troca-se a linha k com a linha r , onde r é tal que :

|a^(k)_{r k}| = max_{{ i = k ,..., n }} | a^(k)_ik |

isto, como é claro, só no caso de k =/= r .

PESQUISA TOTAL DE PIVOT :
Em cada Passo k da eliminação de Gauss, troca-se a linha k com a linha r e a coluna k com a linha s , onde r, s são tais que :

|a^(k)_{r s}| = max_{{ i, j = k ,..., n }} | a^(k)_{i j} |

isto, como é claro, só no caso de k =/= r ou k =/= s .