___ Métodos Iterativos ____
para Sistemas Não Lineares

Consideremos, por exemplo, um sistema da forma:

x1 - x2 sin ( x1 ) = 0
x1 - x2 + cos ( x1 x2 ) = 0
que se pode escrever na forma mais geral: F ( x ) = 0 com F : Rn ---> Rn .
Neste exemplo, temos
F1(x1, x2) = x1 - x2 sin ( x1 )
F2(x1, x2) = x1 - x2 + cos ( x1 x2 )

De forma análoga ao caso unidimensional, podemos pensar num Método do ponto fixo para Rn, começando por estabelecer a equivalência :

F ( x ) = 0 <==> x = G ( x )
A partir deste momento temos definida uma função iteradora G e obtemos um método do ponto fixo :
Iterada inicial: x(0)
Iterar x(n+1) = G ( x(n))
semelhante ao caso unidimensional.
Para estabelecermos as condições de convergência vamos, de novo, definir a contractividade, agora em Rn.

Definição:
Seja G : D C Rn ---> Rn.
Se ||G(x) - G(y) || < L || x - y || para quaisquer x, y em D e para um certo L < 1,
então diz-se que G é contractiva em D relativamente à norma ||.|| .

Teorema: ( do Ponto Fixo em Rn )
Seja D um conjunto fechado e G : D C Rn ---> Rn,
tal que

(i) G(D) C D ,
(ii) G é contractiva em D,
então existe um e um só ponto fixo z em D, e o método do ponto fixo converge para z, se o vector inicial x(0) pertencer a D.

demonstração :

  • Vamos só ver o caso em que D é limitado, por simplicidade (a demonstração geral é semelhante - ver folhas).

  • É claro que se x(0) pertencer a D, atendendo à hipótese (i) e como x(n+1) = G( x (n)), teremos todos os elementos da sucessão, x(n), em D.
  • Isto é importante para aplicarmos a contractividade, e assim mostrarmos que x(n) é uma sucessão de Cauchy:

    ||x(n+m) - x(n) || = ||G ( x(n+m-1)) - G ( x(n-1)) || < L ||x(n+m-1) - x(n-1) || < ... < Ln ||x(m) - x(0) || ---> 0

    quando m, n tendem para infinito, já que L < 1, e porque ||x(m) - x(0) || é limitado, já que os termos da sucessão estão em D, que assumimos ser limitado.
    Concluimos assim que é uma sucessão de Cauchy num conjunto fechado, logo o limite z pertence a D.

  • É fácil ver que z é o ponto fixo, porque :
    ||x(n+1) - G( z ) || = ||G(x(n)) - G( z ) || < L ||x(n) - z || ----> 0 ou seja, como x(n) converge para o limite z isto implica que x(n) converge também para G( z ). Logo z = G ( z ) .

  • A unicidade do ponto fixo surge por absurdo, já que se existissem dois pontos fixos distintos z, w em D, então:
    ||z - w || = ||G(z) - G( w ) || < L ||z - w ||

    ora se eles são distintos podemos dividir por ||z - w || e obtemos L > 1 , o que contradiz a hipótese de contractividade!

    Corolário:
    Da demonstração anterior podemos deduzir as seguintes majorações para os erros:

    || e(n+1) || < L || e(n) ||
    || e(n) || < Ln || e(0) ||
    || e(n+1) || < Ln / ( 1 - L ) || x(1) - x(0) ||

    Observação:
    O caso dos métodos iterativos para sistemas lineares, que vimos, podem ser englobados neste contexto considerando

    x = G (x) = M-1b - M-1N x

    Para exigir que G seja contractiva, como
    || G ( x ) - G ( y )|| = || M-1b + C x - (M-1b + C y)|| =
    = || C ( x - y ) || < ||C|| || x - y ||
    basta que ||C|| < 1, condição que já tinhamos obtido.
    Finalmente, notamos que, como Rn é fechado, podemos aplicar o teorema do ponto fixo para um qualquer x(0) em Rn.

    Para verificarmos que uma função é contractiva, não é necessário usar sempre a definição. Tal como no caso unidimensional, em que utilizamos a derivada, podemos aqui estabelecer uma condição suficiente, mais simples, que envolve agora a noção de matriz Jacobiana :

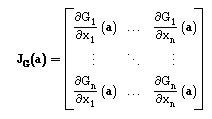
    Teorema:
    Seja D um conjunto fechado e convexo em Rn, e seja G é uma função C1(D).
    Se

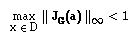
    então a função G é contractiva em D, para a norma do máximo.

    Método de Newton Generalizado

    De forma análoga ao que fizemos no caso unidimensional, podemos deduzir aqui um método, inspirado no método de Newton, cuja ordem de convergência é usualmente quadrática.

    Pretende-se resolver F ( x ) = 0 e reparamos que se pode estabelecer, numa vizinhança da solução, a equivalência

    F ( x ) = 0 <==> x = x - JF-1( x ) F ( x )
    bastando para isso que a função vectorial F seja de classe C1 e que det [JF-1( x )] =/= 0, nessa vizinhança.

    Podemos assim definir uma função iteradora G( x ) = x - JF-1( x ) F ( x ) a que aplicamos o método do ponto fixo.
    Se quisermos verificar que o método converge, podemos usar o teorema do ponto fixo aplicado à função G, já que no caso vectorial não há critérios simplificados para o método de Newton, como estabelecemos para uma dimensão!

  • Para evitar o cálculo "pesado" da inversa da matriz jacobiana, podemos fazer uma pequena alteração no método, de forma a substituirmos o cálculo da inversa pela resolução de um sistema.
    O método de Newton generalizado fica então :
    Iterada inicial: x(0)
    Determinar d, resolvendo o sistema linear
    JF(x(k)) d = - F ( x(k))
    x(k+1) = x(k) + d

    Como dissemos, a convergência deste método, a existir, é (normalmente) quadrática, tendo-se:

    || z - x(k+1) || < K || z - x(k) ||2