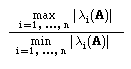Normas de Matrizes e Condicionamento

Para além do problema de instabilidade numérica que decorre da propagação dos erros de arredondamento, podem também ocorrer problemas de mau condicionamento.
Para podermos analisar convenientemente o problema do condicionamento, é necessário introduzirmos a noção de normas vectoriais e matriciais.

Definição:
Seja ||.|| uma norma vectorial em Rn.
A norma da matriz A induzida pela norma vectorial é:

|| A || = max||x||=1 || A x ||
Propriedades :
Para quaisquer matrizes A, B quadradas e qualquer vector x, temos:
i) || A B || < || A || || B ||
ii) || A x || < || A || || x ||

Exemplos de Normas :

1) Norma do Máximo:

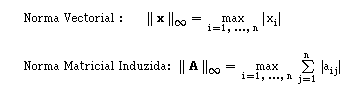
Corresponde ao máximo dos somatórios dos módulos dos elementos das linhas.

2) Norma da Soma:

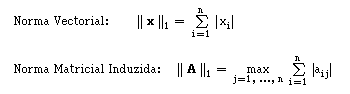
Corresponde ao máximo dos somatórios dos módulos dos elementos das colunas.

3) Norma Euclidiana:



Definição:
Designamos por Raio espectral de uma matriz A o valor :

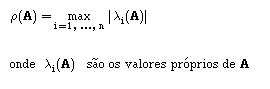
Observação: Se a matriz A fôr simétrica então || A ||2 = 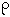(A).


Teorema:
Seja A uma matriz quadrada.
  • Para qualquer norma matricial ||.|| , temos
    (A) < || A ||
  • Para qualquer c > 0 existe sempre uma norma tal que:
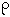    || A ||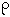 < (A) + c

    Ou seja, o raio espectral é o ínfimo do conjunto das normas de uma matriz.

    Número de Condição de uma Matriz

    Já vimos que ao resolver um sistema

    A x = b
    podemos ter problemas de estabilidade numérica, e para minorar esses problemas, considerámos técnicas de pesquisa de pivot.
    No entanto, se o problema fôr mal condicionado, essas técnicas de pesquisa de pivot deixam de ser úteis, já que um problema mal condicionado será sempre numericamente instável. Interessa-nos, portanto, identificar quais os sistemas que nos podem trazer problemas de condicionamento.

    Supondo que nos era dado, não o vector b exacto, mas apenas uma aproximação b~, vamos analisar a influência desse erro nos resultados obtidos, já que em vez do valor exacto, obtemos um valor aproximado x~, solução do sistema:

    A x~ = b~

    As normas que acabámos de estudar, permitem-nos estabelecer uma medida de comparação entre os erros vectoriais, definindo-se, de forma semelhante ao caso escalar:

  • Erro Absoluto de x~ : || ex || = || x - x~ ||

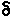  • Erro Relativo de x~ : || x || = || x - x~ || / || x ||

    relativamente a uma certa norma || . || .

    Para estabelecermos a relação entre os erros relativos dos dados e os erros relativos dos resultados vai ser importante estabelecer uma noção que envolve a norma de matrizes :

    Definição:
    Designa-se por Número de Condição de uma matriz A relativamente à norma || . ||, o valor :

    cond (A) = || A || || A-1||

    Teorema:
    Temos as seguintes desigualdades, para o erro absoluto:

    a) || eb || || A ||-1 < || ex || < || A-1 || || eb ||
    e para o erro relativo :
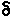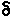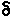    b) || b || cond( A )-1 < || x || < cond( A ) || b ||

    dem:
    Usando os dois sistemas, retiramos

    A ( x - x~) = b - b~
    portanto:
    || A || || x - x~ || > || b - b~ ||
    e
    || x - x~ || < || A-1|| || b - b~ ||
    logo a alínea a) fica provada, pois :
    || A||-1 || b - b~ || < || x - x~|| < || A-1|| || b - b~ ||

    Por outro lado, de A x = b, retiramos, de forma análoga :

    || A||-1 || b || < || x || < || A-1|| || b ||

    dividindo o resultado de a) por este resultado, obtemos b).

    Observações:
    1) Como é óbvio, podemos concretizar estes resultados para qualquer uma das normas.
    Por exemplo, podemos retirar a majoração :

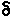    || x ||1 < cond1( A ) || 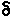b ||1
    onde cond1( A ) designa o número de condição relativamente à norma da soma, ou seja :
    cond1( A ) = || A ||1 || A-1||1

    2) Se || I || = 1 (o que acontece para as normas estudadas), como || I || = || A A-1 || < || A || || A-1 || ,
    obtemos cond( A ) > 1.

  • Destes resultados podemos concluir que um número de condição elevado não nos permite estabelecer boas majorações para o erro relativo.
    Quanto maior fôr o número de condição, pior será a majoração de erro relativo obtida.

    Consequentemente, para matrizes cujo número de condição seja elevado, um pequeno erro relativo no vector b, pode provocar um grande erro relativo na solução do sistema.

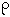  • Terminamos este parágrafo observando que podemos também definir um número de condição associado ao raio espectral :
    cond 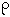( A ) = ( A ) 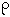( A-1 )

    que verifica a propriedade (resultante do raio espectral ser o ínfimo das normas) :

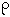    cond ( A ) < cond ( A )
    para qualquer norma.

    Atendendo a que os valores próprios de A-1 são os inversos de A, temos :

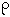    cond ( A ) =