Métodos de Factorização

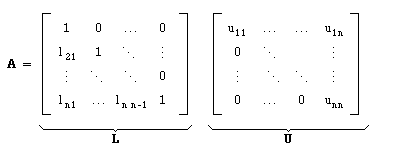
Vimos no Teorema II.1.1 que usando o Método de Eliminação de Gauss, no caso de não haver troca de linhas, podemos obter uma factorização da matriz A na forma A = L U , onde U seria a matriz triangular superior obtida no final da factorização e L a matriz triangular inferior com diagonal unitária, cujos elementos seriam os multiplicadores m_ik.

Vamos agora ver uma maneira alternativa de obter essa mesma factorização através do Método de Doolittle.

Método de Doolittle

Pretendemos obter as matrizes L e U tais que A = L U

Logo, efectuando o produto, podemos obter as fórmulas correspondentes ao método de Doolittle:

PASSO 1 :

u_{1 j} = a_{1 j}	( j = 1, ..., n )
l_{i 1} = a_{i 1} / u₁₁	( i = 2, ..., n )

PASSO k :

u_{k j} = a_{k j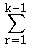} - l_{k r} u_{r j}	( j = k , ..., n )
l _{i k} = ( a_{i k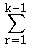} - l_{i r} u_{r k}) / u_{k k}	( i = k+1 , ..., n )

Para factorizar a matriz, usando o método de Doolittle são necessárias o mesmo número de operações que no método de eliminação de Gauss. Há, no entanto, vantagens apreciáveis no que diz respeito ao armazenamento dos elementos da matriz, já que estes não são sucessivamente alterados, como acontecia no caso do método de Gauss.
(Para este método também se pode utilizar uma pesquisa de pivot (por colunas) antes de se efectuar a divisão correpondente ao cálculo dos elementos de L).

Observação: De forma semelhante, podemos pensar numa factorização em que ao invés de L, será a matriz U que terá a diagonal principal unitária. Esse outro processo, em tudo semelhante a este, dá origem ao Método de Crout.

Vamos agora ver alguns métodos particulares para certo tipos de matrizes, em que podemos reduzir o números de operações. Começamos pelas matrizes simétricas e depois vamos ver o caso das matrizes tridiagonais.

Método de Cholesky

Como trabalhamos com números reais, só pode ser aplicado a matrizes:

Simétricas ( A = A^T)

Definidas Positivas

Relembrando que uma matriz é definida positiva se:

x^TA x > 0 , para todo o x=/=0

ou, se os valores próprios são positivos.

ou, se os menores principais são positivos.

Mas, na prática, como é claro só para verificar que a matriz é definida positiva perderiamos mais tempo do que a resolver o sistema...
Assim, o método só é aplicado a matrizes que sabemos, à partida (por exemplo, por resultados teóricos), serem definidas positivas e simétricas.

Para este tipo de matrizes é válida a factorização: A = L L^T,
e o método consiste nos seguintes passos:

PASSO 1:

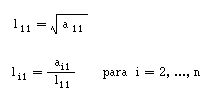
PASSO k:

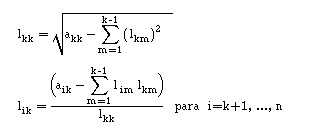
Neste caso, o número de operações é :

~ n³ / 6	Somas + Subtracções
~ n³ / 6	Multiplicações + Divisões
n	Raízes Quadradas

Matrizes Tridiagonais

Este é o caso de matrizes em que, à excepção das três diagonais principais, todos os outros elementos são nulos. Ou seja: a_ij = 0, se | i - j | > 1

Estas matrizes aparecem em muitos problemas práticos (por exemplo, no caso dos splines, ou na resolução de equações às derivadas parciais...) .

Devido à sua estrutura simples, o número de operações necessário para resolver um sistema, pode ser consideravelmente reduzido, já que podemos escrever A = L U; onde L será uma matriz triangular inferior, bidiagonal, com diagonal unitária, e U uma matriz triangular superior, bidigonal.

O método de factorização de Doolittle reduz-se então a:

Passo 1:

l₁₁ = 1

l₂₁ = a₂₁

u₁₁ = a₁₁

u₁₂ = a₁₂

Passo k
(k = 2, ..., n)

l_kk=1	u_kk = a_kk - l_{k, k-1} u_k-1,k
l_{k+1, k} = a_{k+1, k} / u_kk	u_{k, k+1} = a_{k, k+1}

Podemos contabilizar o número de operações efectuado na factorização e na resolução dos sistemas triangulares (neste caso, a substituição ainda será mais simples):

.	Somas + Subtracções	Multipl. + Divisões
Factorização	n - 1	2n - 2
Resolver Lg = b	n - 1	n - 1
Resolver Ux = g	n - 1	2 n - 1
TOTAL	3 n -3	5 n - 4

Correspondendo a um total de ~8n operações!