___ Métodos Iterativos ____
para Sistemas Lineares

Neste parágrafo, o objectivo é encontrar métodos que permitam aproximar a solução de um sistema linear, por forma a diminuir o número de operações (relativamente aos métodos directos), o que pode ser útil no caso de se tratar de um sistema com um grande número de equações, especialmente se a matriz possuir muitos elementos nulos.

Outra vantagem dos métodos iterativos é evitar os problemas de instabilidade numérica, que podem ocorrer num método directo.

Consideremos então um sistema genérico

A x = b

vamos escrever A = M + N

e obtemos (M+N) x = b < = > x = M-1b - M-1N x

Daqui podemos retirar um método iterativo que consiste em:

Escolher um vector inicial x(0)
Iterar x(k+1) = M-1b - M-1 N x(k)

É importante que a matriz M seja muito mais simples do que A, porque senão não estariamos a simplificar o problema...

Note-se que esta iteração pode ser feita de outra forma, não havendo necessidade de se proceder verdadeiramente ao cálculo da inversa de M.

  • De entre os métodos iterativos, destacam-se dois métodos, o método de Jacobi, e o método de Gauss-Seidel.

    Consideramos a matriz A decomposta na soma de três matrizes A = L + D +U, onde L é a matriz triangular inferior, U a matriz triangular superior, ambas com zeros na diagonal principal e D a matriz diagonal.

    Notamos que a matriz diagonal D não poderá ter zeros na diagonal principal. Caso isso aconteça, deve-se efectuar uma troca de linhas ou colunas na matriz A, para obtermos uma matriz D adequada.

    Método de Jacobi

    No caso do método de Jacobi, consideramos
    M = D
    N = L+ U
    Portanto, o método consiste em

    Iterada inicial x(0)
    Iterar x(k+1) = D-1b - D-1 (L + U) x(k)
    ou ainda

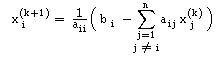
    Método de Gauss-Seidel

    No caso do método de Gauss-Seidel, consideramos
    M = L + D
    N = U
    Portanto o método consiste em

    Iterada inicial x(0)
    Iterar x(k+1) = D-1b - D-1 L x(k+1) - D-1 U x(k)
    ou ainda

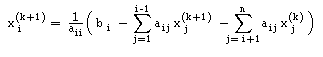
    Número de Operações:
    A menos que as matrizes possuam zonas apreciáveis com elementos nulos, ambos os métodos iterativos exigem um cálculo total de ~ 2n2 operações, por cada iterada, o que implica que, se forem necessárias mais que ~ n/3 iterações, exigimos mais operações do que num método directo.
    Ainda assim, pode ser conveniente a utilização de métodos iterativos, para evitar problemas de estabilidade numérica.

    Critérios de convergência

    Vamos agora estabelecer critérios que nos permitam determinar quando existe convergência para estes métodos iterativos.
    Começamos por reparar que
    x(k+1) = M-1 b - M-1N x(k)
    x = M-1 b - M-1N x
    de onde retiramos
    e(k+1) = x - x(k+1) = - M-1 N ( x - x(k)) = C e(k)
    designando C = - M-1N .

    Aplicando sucessivamente, obtemos
    e(k) = Ck e(0)

    ou seja, o erro convergirá para o vector nulo (para uma qualquer iterada inicial) se as sucessivas potências da matriz C tenderem para a matriz nula.

    Isto pode ser verificado, mais facilmente, usando o:

    Teorema : ( Condições Necessárias e Suficientes de Convergência )
    Qualquer que seja o vector inicial x(0) os métodos iterativos convergem
    sse

    a) O raio espectral da matriz C fôr menor que 1.
    sse
    b) Existe uma norma ||.|| : ||C|| < 1

  • Método de Jacobi, C = - D-1( L + U )
  • Método de Gauss-Seidel, C = - ( L + D )-1 U

    Corolário:
    Temos as seguintes majorações para os erros:

    || e(k+1) || < || C || || e(k) ||
    || e(k) || < || C ||k || e(0) ||
    || e(k+1) || < || C || / ( 1 - || C || ) || x(k+1) - x(k) ||

    Observação:
    Podemos falar também de ordem de convergência, no caso vectorial, e estas majorações revelam que estes métodos iterativos têm uma convergência linear .

    Critérios Suficientes de Convergência

    Para além do teorema, que nos dá condições necessárias e suficientes de convergência, existem critérios mais simples que asseguram a convergência para qualquer iterada inicial. No entanto, essas condições, que iremos deduzir, são apenas condições suficientes.

    Repare-se, por exemplo, no caso do método de Jacobi. Como C = D-1 ( L + U )

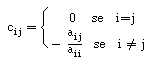
    e relembrando que

    ao exigirmos que a norma seja inferior a 1, isto significa
    Logo, uma condição suficiente que nos garante isso, é
    neste caso, diz-se que a matriz A tem diagonal estritamente dominante por linhas.

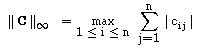
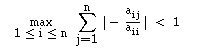
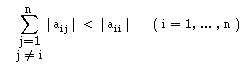
    Da mesma forma, considerando a norma ||.||1, podemos concluir que se

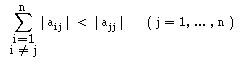
    isto é, se a matriz A tem diagonal estritamente dominante por colunas, então o método de Jacobi converge.

    Este raciocínio pode-se aplicar também ao método de Gauss-Seidel e obtemos :



    Teorema : ( Condição Suficiente de Convergência )
    Se a matriz A tiver a diagonal estritamente dominante por linhas ou por colunas, os métodos de Jacobi e de Gauss-Seidel convergem, para qualquer vector inicial x(0) escolhido.

    Observação:
    Como C = M-1N = M-1 ( A - M ) = I - M-1A quanto mais próxima de A fôr a matriz M, mais próximo da matriz zero será valor de C, e consequentemente, mais rápida será a convergência do método iterativo.

    Nos casos dos métodos que estudamos, "intui-se" que M está "mais próxima" de A no caso do Método de Gauss-Seidel (M = L + D ) do que no caso do Método de Jacobi ( M = D ).

    Portanto, "de um modo geral" o método de Gauss-Seidel converge mais rapidamente. Há, no entanto, casos em que isso não acontece, e um método pode convergir e o outro não!