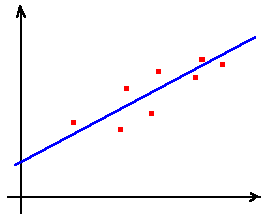
Regressão Linear: Neste caso pretendemos encontrar a função do tipo a + b x
(... ou seja, a recta) que "melhor se adapta" aos valores dados.
|
|
Neste parágrafo vamos estudar a aproximação de funções numa perspectiva diferente da interpolação. Por exemplo, se tivermos apenas os valores da função em certos pontos, não vamos exigir que a função aproximadora interpole a função dada nos pontos. Exigimos apenas que essa função aproximadora tome valores (nesses pontos) de forma a minimizar a distância aos valores dados... falamos em minimizar, no sentido dos mínimos quadrados!
Isto é importante em termos de aplicações, já que podemos ter valores obtidos, experimentalmente, com uma certa incerteza. Ao tentar modelizar essa experiência, com uma certa classe de funções, seria inadequado exigir que a função aproximadora interpolasse esses pontos.
Um caso simples, em que se aplica esta teoria é o caso da regressão linear, em que tentamos adaptar a um conjunto de pontos e valores dados, a "melhor recta", que (neste caso) será a recta que minimiza a soma quadrática das diferenças entre os valores dados ao valores da recta, nesses pontos.

Esta é uma perspectiva discreta, em que o conjunto de valores dados é finito.
Podemos também pensar num caso contínuo, em que apesar de conhecermos
a função, não apenas em certos pontos, mas em todo um intervalo, estamos interessados
em aproximar essa função (... no sentido dos mínimos quadrados) por funções de uma outra
classe, mais adequada ao problema que pretendemos resolver. Por exemplo, podemos
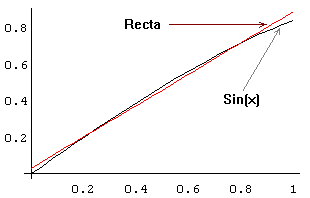
estar interessados em determinar qual a "melhor recta" que aproxima a função sin(x) no
intervalo [0, 1] ...
Consideremos, de novo, um conjunto de pontos x0 , ... , xn a que estão associados, respectivamente, os valores f(x0) , ... , f(xn) .
Temos que considerar agora uma classe de funções, entre as quais vamos tentar encontrar a que "melhor aproxima" aquele conjunto de valores, nos pontos dados.
Vamo-nos concentrar em funções da forma:
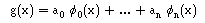
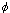 0(x), ... ,
0(x), ... , 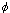 n(x)
são funções base (linearmente independentes), e são conhecidas.
n(x)
são funções base (linearmente independentes), e são conhecidas.
Neste caso, apenas teremos que determinar os parâmetros a0 , ... , an , de forma a que a soma quadrática das diferenças entre os f( xi ) e os g( xi ) seja mínima. Faz pois sentido introduzir a norma :
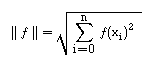
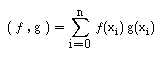
Pretende-se pois encontrar os parâmetros a0 , ... , an que minimizem a distância entre f e g , ou, o que é equivalente, minimizem :
Para obtermos esse mínimo, começamos por procurar os valores a0 , ... , an tais que todas as derivadas parciais de Q sejam nulas, isto é:
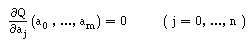
Calculamos a derivada parcial, usando as propriedades da derivação do produto interno :
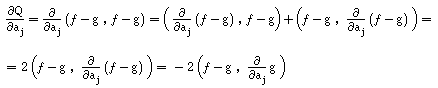
Por outro lado
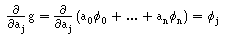
e assim obtemos, para cada j de 0 até m :
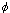 j ) = 0
j ) = 0
Podemos ainda substituir a expressão de g e obtemos um sistema linear :
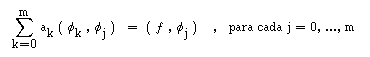 |
designado por Sistema Normal, que escrevemos matricialmente :
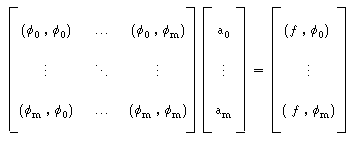 |
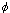 0 , ... ,
0 , ... , 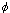 m
forem linearmente independentes.
m
forem linearmente independentes.
Exemplo: No caso de considerarmos a aproximação através de funções polinomiais,
temos como funções base, 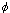 0 = 1, ... ,
0 = 1, ... ,
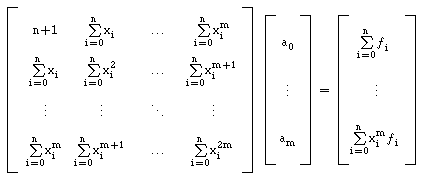
 m = xm,
e assim obtemos:
m = xm,
e assim obtemos:
Observações:
 i ,
i ,
 j) =
j) =
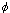 i ( x0 )
i ( x0 )
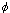 j ( x0 ) +
... +
j ( x0 ) +
... +
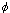 i ( xn )
i ( xn )
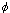 j ( xn )
j ( xn )
podemos reparar que se trata de um produto na forma XTX , em que X é a matriz n x m :
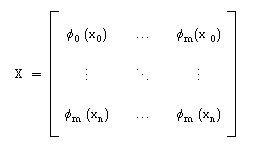
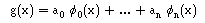
A única diferença existente, face ao caso discreto, está na norma e no produto interno :

Tudo se deduz de forma semelhante, e obtemos também um sistema normal, cuja única diferença está no significado dos produtos internos.
Exemplo:
No caso em que consideramos como funções base, os
polinómios, 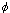 0 = 1, ... ,
0 = 1, ... ,
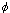 m = xm,
obtemos agora o sistema normal
m = xm,
obtemos agora o sistema normal
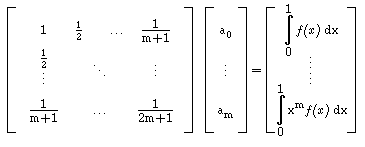
Esta matriz designa-se Matriz de Hilbert, e é extremamente mal condicionada. Com efeito, já para m = 3 obtemos Cond1 = 28375, e para m = 4 já atinge 943656, continuando a crescer fortemente! Temos, assim, problemas de condicionamento e consequentemente de instabilidade numérica, para este tipo de matrizes.
Existe uma analogia geométrica entre os Met. Mínimos Quadrados e a determinação
do ponto de um plano que se encontra a menor distância de um outro, exterior
ao plano.
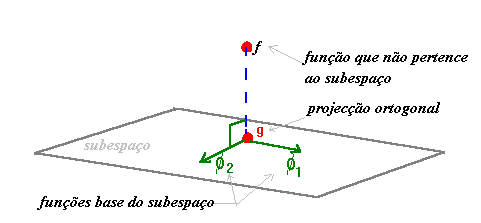
Através de um produto interno podemos falar na projecção ortogonal, e relembramos que, exigir:
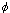 j ) = 0
j ) = 0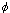 j .
j .