MÉTODO de NEWTON

Pode ser encarado como um caso particular do método do ponto fixo, onde é possível obter uma convergência quadrática. Basta reparar que se f '(z) =/= 0:

f(z) = 0 <=> z = z - f(z) / f '(z)

definindo a função iteradora g(z) = z - f(z) / f '(z), e os pontos fixos de g serão os zeros de f.
Para além disso, podemos ver que :

g'(z) = f(z) f ''(z) / ( f ' (z) )2

ora como f(z) = 0 então g'(z) = 0 . Pelo teorema anterior, usando esta função iteradora g, é possível arranjar uma vizinhança da raiz onde asseguramos, pelo menos, uma convergência quadrática (desde que f ' (z) =/= 0).

Portanto o método de Newton resume-se a efectuar as iterações:

Iterada inicial: x0
xn+1 = xn - f(xn ) / f ' (xn )

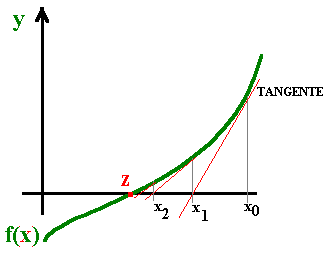
Historicamente, a origem do método de Newton é geométrica.
Consiste em definir a nova iterada a partir da intersecção com o eixo das abcissas da tangente à função f (calculada na iterada anterior) :

basta reparar que a equação da tangente num ponto xn é
y = f(xn ) + f ' (xn ) ( x - xn )
e a iterada xn+1 é a "raiz da tangente", basta pois fazer y = 0 para verificarmos que o valor de xn+1 coincide com o obtido.

É também claro, mesmo geometricamente, que não podemos ter iteradas em que f ' (xn) = 0, pois ficariamos com tangentes paralelas ao eixo das abcissas, que nunca o intersectariam (... na "nossa" geometria euclidiana!).






Para assegurar a convergência, podiamos aplicar o teorema do ponto fixo à função g do método de Newton, mas podemos estabelecer um critério mais simples :

Teorema (Condições Suficientes de Convergência para o Método de Newton):
Seja f uma função C2[a, b] que verifique :

1) f(a) f(b) < 0
2) f ' (x) =/= 0 para qualquer x em [a,b]
3) f ''(x) > 0 ou f ''(x) < 0 para qualquer x em [a,b]

4a) | f(a) / f '(a) | < | a - b | e também | f(b) / f '(b) | < | a - b |
ou
4b) f(x0 ) f ''(x) > 0 para qualquer x em [a, b]

então:
a equação f(x) = 0 tem uma solução única z pertencente ao intervalo [a,b] e o método de Newton converge para essa solução :

  • qualquer que seja o x0 pertencente a [a,b] se se verificar 4a)
  • para os x0 em [a,b] que verificarem 4b).

    Fórmula do Erro do Método de Newton

    Obtém-se, facilmente, através do desenvolvimento em série de Taylor (em torno de xn):

    f(z) = f(xn) + f'(xn ) (z - xn) + ½ f''(§m ) (z - xn )2
    para um certo §m no intervalo aberto cujos extremos são z e xn.

    Dividindo por f ' (xn ), não nulo, ficamos com:

    portanto

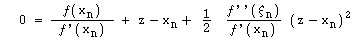
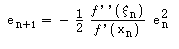
    na prática, se tivermos assegurado as condições de convergência num intervalo [a,b], podemos garantir:


    Proposição: (Convergência Local)
    Seja f uma função C2( I ), onde I é um intervalo que é vizinhança da raiz z.
    Se f '(z) =/= 0, então a sucessão definida pelo método de Newton converge para z (desde que x0 seja suficientemente próximo de z ), e temos convergência quadrática:
    (o coeficiente assimptótico de convergência será o módulo deste valor).

    MÉTODO da SECANTE

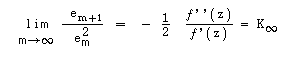
    É muito semelhante ao Método de Newton, mas substitui o cálculo das derivadas pelo cálculo de uma razão incremental.
    Geometricamente, corresponde a substituir o papel da tangente, no método de Newton, por uma secante (de onde vem o nome).
    É claro que isto significa que vamos precisar sempre de dois pontos para a determinar, o que implica que tenhamos que considerar duas iteradas iniciais, que designamos por x-1 e x0.

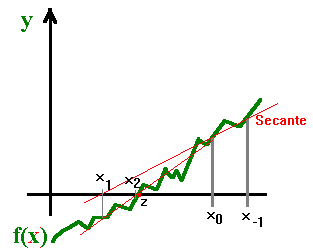
    De forma semelhante à que fizemos no método de Newton, calculando agora o ponto de intersecção da secante com o eixo das abcissas, obtemos a fórmula para xn+1, e o método da secante fica:

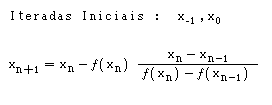    Condições Suficientes de Convergência:

    São idênticas às enunciadas para o Método de Newton, apenas a condição 4b) deverá ser substituída por

    4b' ) f(x0 ) f ''(x) > 0 e também f(x-1 ) f ''(x) > 0 para qualquer x em [a, b]

    Fórmula do Erro :

    Neste caso a ordem de convergência é supra-linear mas não é quadrática.
    ( Usando logaritmos, e o facto que o limite da razão de uma sucessão de Fibonacci é o número de ouro p=1.61803... pode-se verificar que a ordem de convergência dá exactamente este valor.)