O integral (continuação).
Critérios de integrabilidade (conclusão):
Funções nulas excepto num número finito de pontos.
Propriedades elementares do integral:
Linearidade, aditividade em relação ao intervalo de integração, monotonia do integral.
Consequências: independência relativamente aos valores num conjunto finito de pontos, funções seccionalmente cobtínuas.
O teorema da média.
Material de estudo:
Nesta aula continuamos o estudo do integral, focando-nos desta vez nas propriedades elementares do integral. Na próxima aula será estudado o Teorema Fundamental do Cálculo (TFC) que nos dará uma forma sistemática de cálculo de integrais. Mas antes, precisamos de resultados que vão ser importantes quer para a obtenção desse teorema quer para aplicação ao cálculo prático de integrais em conjunto com o TFC.
O estudo do material desta aula terá como objectivo compreender as propriedades elementares do integral dadas e saber como aplicar ao cálculo de integrais.
Os exercícios resolvidos da lista [I] correspondente a esta aula são ainda os mesmos da aula anterior.
Para isso fornecem-se alguns primeiros exemplos embora estas propriedades venham a ser posteriormente usadas de forma sistemática.
O material desta aula, nomeadamente as demonstrações que omitimos, pode ser encontrado no texto [AB], páginas 117-121.
Incentiva-se os alunos a visualizarem as aulas em video [MA] 24 e 1ª parte da aula 25.
O próximo exemplo ilustra a afirmação intuitiva "a área de uma linha é zero":
Exemplo. \(f(x)=\begin{cases}0 &\text{ se } x\in [0,2]\setminus\{1\},\\ 10 &\text{ se }x=1, \end{cases}\quad\) ou seja, no intervalo \(I=[0,2]\), \(f(x)=0\) excepto em \(x=1\), onde \(f(1)=10.\)
Consideremos a decomposição \(\;d_n=\{1-\frac{1}{n}, 1+\frac{1}{n}\}.\;\) A ideia é "isolar" o ponto \(x=1\) num subintervalo cujo comprimento tende para 0 quando \(n\to\infty.\). Os subintervalos serão \[I_1=\left[0,1-\frac{1}{n}\right],\qquad I_2=\left[1-\frac{1}{n}, 1+\frac{1}{n}\right],\qquad I_3=\left[1+\frac{1}{n}, 2\right].\]
Logo, \[m_1=\inf f(I_1)=0,\qquad m_2=\inf f(I_2)=0,\qquad m_3=\inf f(I_3)=0,\] \[M_1=\sup f(I_1)=0,\qquad M_2=\sup f(I_2)=10,\qquad M_3=\sup f(I_3)=0.\] \[x_1-x_0=1-\frac{1}{n},\qquad x_2-x_1=\frac{2}{n},\qquad x_3-x_2=1-\frac{1}{n}\]As somas inferior e superior relativas a esta decomposição serão então: \[\begin{aligned} s_{d_n}&=m_1(x_1-x_0)+m_2(x_2-x_1)+m_3(x_3-x_2)=0,\\ S_{d_n}&=M_1(x_1-x_0)+M_2(x_2-x_1)+M_3(x_3-x_2)=\frac{20}{n}. \end{aligned}\] Assim, \(S_{d_n}-s_{d_n}\to 0\) e, portanto, pelo último corolário da aula anterior, \(f\) é integrável em \(I\) com integral \[\int_0^2 f(x)\,dx=\lim_{n\to\infty}s_{d_n}=\lim_{n\to \infty}S_{d_n}=0\,.\]
Este argumento pode ser inteiramente reproduzido para qualquer função que seja nula num intervalo excepto num ponto desse intervalo. Se, em vez de um,
tivermos um número finito de pontos onde \(f(x)\) não é nula, adaptamos este procedimento considerando decomposições \(d_n\) que "isolem" cada um desses pontos.
Exemplo: Se \(f(x)=0\) em \(I=[0,9]\) excepto em \(\{2,4\}\) e \(f(2)=1\), \(f(4)=-1\), escolhemos
\(\;d_n=\{2-\frac{1}{n},2+\frac{1}{n},4-\frac{1}{n},4+\frac{1}{n}\}\;\). Como exercício escreva \(s_{d_n}, S_{d_n}\) e complete o argumento.
Mais geralmente temos então:
Proposição.Seja \(\;I=[a,b],\;\) com \(\;a\lt b\;\) finitos. Se \(\;f(x)=0\;\) em \(\;I\;\) excepto em \(\;x=c_1,\dots,c_p\;\) (conjunto finito), então \(\;f\;\) é integrável em \(\;I\;\) e \[\int_a^b f(x)\, dx=0\,.\]
Proposição (linearidade do integral).Sejam \(\;f,g\;\) funções integráveis em \(\;[a,b]\;\) e \(\;c\;\) uma constante real. Então, \(\;f\pm g\;\) e \(\;cf\;\) são integráveis em \(\;[a,b]\;\) e \[\int_a^b(f\pm g)(x)\,dx=\int_a^b f(x)\,dx\pm \int_a^b g(x)\,dx\,,\] \[\int_a^b(cf)(x)\,dx=c\int_a^b f(x)\,dx .\]
A demonstração desta propriedade, tal como as demonstrações das outras propriedades elementares do integral, parte da propriedade correspondente para as somas inferiores e superiores e, a partir daí, passa-se para a do integral por enquadramento deste entre as somas inferiores e superiores. Pode ver a demonstração deste resultado em [AB] (Teorema 4.3.6).
Exemplo Da aula anterior sabemos que \[\int_0^1 1\,dx=1,\qquad \int_0^1 x\,dx=\frac{1}{2},\qquad \int_0^1 x^2\,dx=\frac{1}{3}.\] Usando a proposição anterior e estes integrais podemos calcular, por exemplo, \[\int_0^1(5+6x+9x^2)\,dx=5\int_0^1 1\,dx+6\int_0^1 x\,dx+9\int_0^1 x^2\,dx=5+3+2=10\,.\]
Uma consequência importante desta propriedade é a seguinte:
Corolário (o integral não depende dos valores num conjunto finito de pontos).Se \(\;f\;\) é integrável em \(\;[a,b]\;\) e \(\;g(x)=f(x)\;\) excepto quando \(\;x=c_1,\dots,c_p\;\) (conjunto finito), então \(\;g\;\) é integrável em \(\;[a,b]\;\) e \[\int_a^b g(x)\,dx=\int_a^b f(x)\,dx.\]
Resulta do facto de que a função \(\;h(x)=f(x)-g(x)\;\) é nula excepto naquele conjunto de pontos e portanto, pela 1ª proposição da aula, é integrável com integral nulo. Da linearidade do integral sai então o resultado.
Proposição (aditividade em relação ao intervalo de integração).
- Se \(\;f\;\) é integrável em \(\;[a,b]\;\) então é integrável em qualquer intervalo \(\;[c,d]\subset [a,b].\)
- Se \(\;f\;\) é integrável em \(\;[a,c]\;\) e em \(\;[c,b]\;\) então é integrável em \(\;[a,b]\;\) e \[\int_a^b f(x)\,dx=\int_a^c f(x)\,dx+\int_c^b f(x)\,dx\]
Exemplo Considere a função \(f\) seguinte com uma descontinuidade em \(x=1\):
\[f(x)=\begin{cases}x^2&\text{ se } 0\leqslant x \lt 1\\
-2&\text{ se } 1\leqslant x \leqslant 2.\end{cases}\,\quad\]
Dizer se \(f\) é integrável em \([0,2]\) e, em caso afirmativo, calcular o integral.
Resposta: No intervalo \([0,1]\), \(f(x)=x^2\) excepto quando \(x=1\) (\(f(1)=-2\)). Logo, pelo corolário atrás, \(f\) é integrável em \([0,1]\).
No intervalo \([1,2]\), \(f(x)=-2\) constante e, portanto é integrável.
Pela última proposição temos então,
\[\int_0^2 f(x)\,dx=\int_0^1 f(x)\,dx+\int_1^2 f(x)\,dx=\int_0^1 x^2\,dx+\int_1^2 (-2)\,dx=\frac{1}{3}-2(2-1)=-\frac{5}{3}.\]
Reparem que o que está em causa neste exemplo é uma função \(f\) contínua em \([a,b]\setminus \{c\}\), com \(a\lt c \lt b\), existindo \(f(c^-),\;f(c^+)\). A existência destes limites laterais permite-nos dizer que, em cada um dos intervalos \([a,c]\) e \([c,b]\) \(f\) coincide em todo o intervalo excepto no ponto \(x=c\) com uma função continua nesses intervalos fechados e podemos aplicar a proposição anterior.
Generalizando este argumento temos,
Proposição (integrabilidade de funções seccionalmente contínuas).Sejam \(\;c_1\lt c_2\lt \dots\lt c_p\;\) pontos interiores de \([a,b]\) (conjunto finito). Se \(\,f\,\) é contínua em \(\;[a,b]\setminus\{c_1,\dots,c_p\},\;\) tal que existem os limites laterais \(\;f(c_1^{\pm}),\dots, f(c_p^{\pm}),\;\) então \(\,f\,\) é integrável em \(\;[a,b]\;\) e \[\int_a^b f(x)\,dx=\int_a^{c_1} f(x)\,dx+\int_{c_1}^{c_2} f(x)\,dx+\dots+\int_{c_p}^b f(x)\,dx.\]
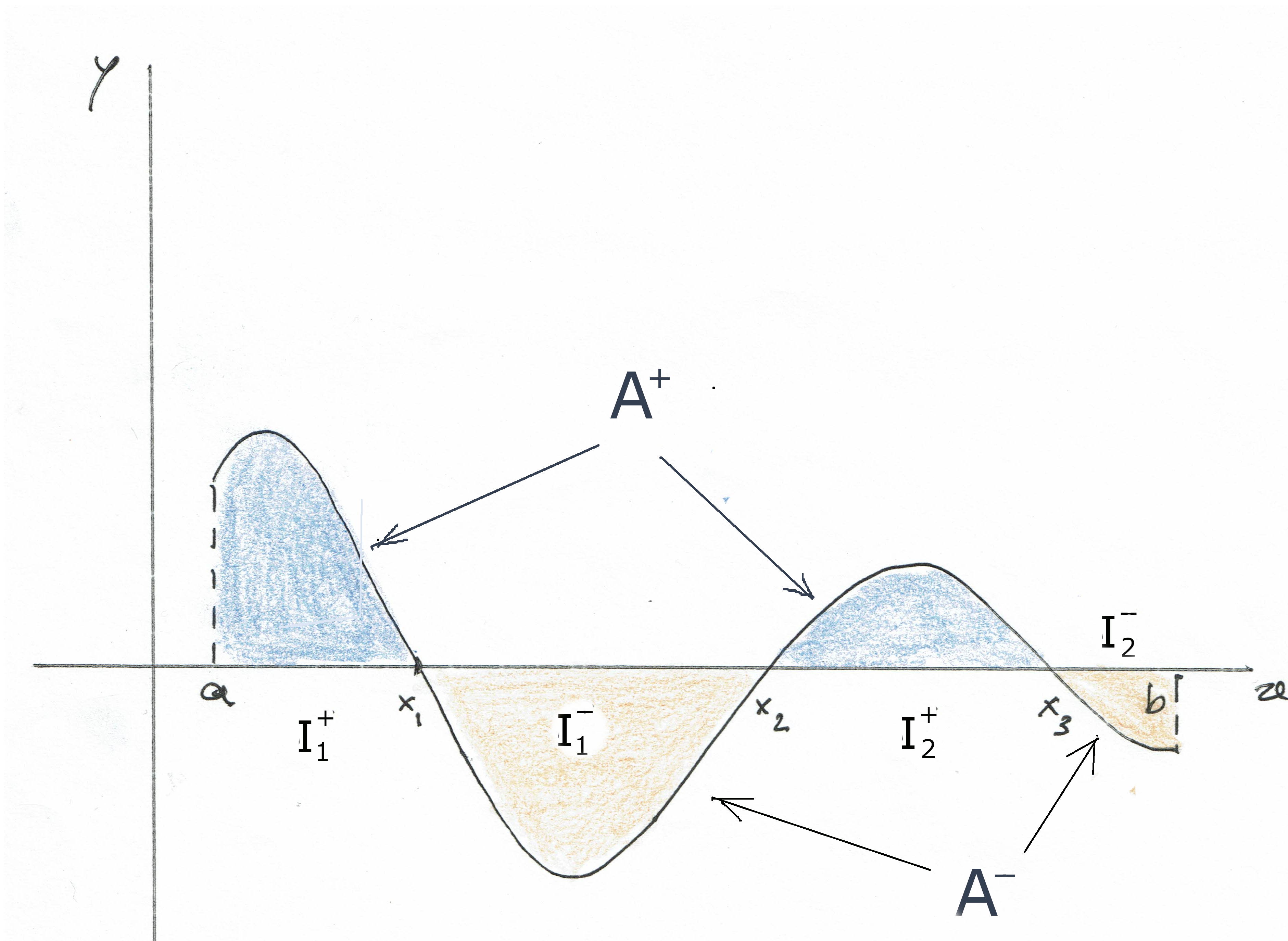
Observações sobre a interpretação do integral como uma área
Suponham que \(f\) é integrável em \(I\) e que \(\;I=I_1^-\cup\dots\cup I_p^-\cup I_1^+\cup\dots\cup I_q^+\;\) com \(\;f(x)\leqslant 0\;\) nos intervalos \(\;I_i^-\;\) e \(\;f(x)\geqslant 0\;\) nos intervalos \(\;I_i^+\;\). Então, \[\begin{aligned}\int_a^b f(x)\,dx&=\sum_{i=1}^p \int_{I_i^-}f(x)\, dx+\sum_{i=1}^q \int_{I_i^+}f(x)\,dx\\ &=-\text{ Área de }A^- + \text{ Área de }A^+\end{aligned}\] em que \(A^-\) é a união dos subconjuntos do semiplano \(y\leqslant 0\) entre o gráfico de \(f\) e o eixo \(0x\) para \(x\) nos intervalos \(I_i^-,\;\) enquanto que \(A^+\) é a união dos subconjuntos do semiplano \(y\geqslant 0\) entre o gráfico de \(f\) e o eixo \(0x\) para \(x\) nos intervalos \(I_i^+.\)

Vamos deduzir uma nova propriedade. Suponhamos agora que \(f\geqslant 0\) em \(I=[a,b]\). Então, dada \(d\), uma decomposição de \(I\) qualquer, em cada um dos subintervalos \(I_i\) teremos \[m_i=\inf f(I_i)\geqslant 0\] e, portanto, \[s_d=\sum_{i=1}^n m_i (x_i-x_{-1})\geqslant 0.\] Como, por definição \(\int_a^b f(x)\,dx \geqslant s_d,\) concluimos a parte 1. do resultado seguinte:
Proposição (monotonia do integral)
- Seja \(f\) integrável em \([a,b]\). Então, \[f\geqslant 0\;\text{ em }\; [a,b]\quad\Rightarrow\quad \int_a^b f(x)\, dx\geqslant 0.\]
- Sejam \(f,g\) integráveis em \([a,b].\) Então, \[f\geqslant g\;\text{ em }\; [a,b]\quad\Rightarrow\quad \int_a^b f(x)\, dx\geqslant \int_a^b g(x)\, dx.\]
A parte 2. resulta da parte 1. aplicando-a à função \(h(x)=f(x)-g(x)\) e usando a linearidade do integral.
Definição (valor médio de uma função).Dada \(f\) integrável em \([a,b]\), define-se o valor médio de \(f\) em \([a,b]\): \[\bar{f}=\frac{1}{b-a}\int_a^b f(x)\,dx.\]
Exemplo: Usando a interpretação geométrica do integral facilmente se conclui que, dados \(a\lt b\) se tem \[\int_a^b x\,dx=\frac{b^2}{2}-\frac{a^2}{2}.\] Temos então, que em \([a,b]\), a média da função \(f(x)=x\) é dada por \[\bar{f}=\frac{1}{b-a}\int_a^b x\,dx=\frac{b^2-a^2}{2(b-a)}=\frac{a+b}{2}.\]
Teorema (da média para funções contínuas)Seja \(f\) uma função contínua em \(\;[a,b]\;\) com \(a\lt b\) finitos. Então, existe \(c\in\left[a,b\right]\) tal que \[\bar{f}=f(c)\]
Por outras palavras, o valor médio da função \(f\) em \([a,b]\) é assumido por \(f\) em algum ponto interior do intervalo \([a,b]\).
Demonstração. Sendo \(f\) contínua no intervalo fechado e limitado \([a,b]\) sabemos, pelo teorema de Weierstrass, que existem \(\;c_1,\,c_2\in [a,b]\) tais que,
\(\;f(c_1)=\min f([a,b])=m\;\) e \(\;f(c_2)=\max f([a,b])=M\;\).
Usando a monotonia do integral vista numa proposição atrás temos,
\[\forall_{x\in[a,b]}\;\; m\leqslant f(x)\leqslant M \quad\Rightarrow\quad \int_a^b m\,dx\leqslant \int_a^b f(x),dx\leqslant \int_a^bM\,dx\]
\[\Rightarrow\quad m(b-a)\leqslant \int_a^b f(x),dx\leqslant M(b-a)\quad\Rightarrow\quad m\leqslant \frac{1}{b-a}\int_a^b f(x)\,dx\leqslant M.\]
ou seja,
\[f(c_1)\leqslant \bar{f}\leqslant f(c_2).\]
Pela continuidade de \(f\) podemos aplicar o teorema de Bolzano e afirmar que existe \(c\) entre \(c_1\) e \(c_2\) tal que
\[f(c)=\bar{f}\]
e o teorema fica demonstrado.
A igualdade \[\frac{1}{b-a}\int_a^b f(x)\,dx=f(c)\] para algum \(c\in\left]a,b\right[\) vai ser de crucial importância para a obtenção do Teorema Fundamental do Cálculo na próxima aula.